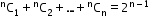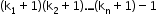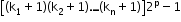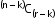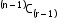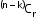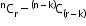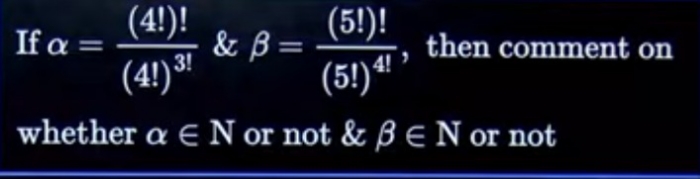JEE Maths Permutations and Combinations

SYNOPSIS

1. Fundamental Principle of Counting
   

   Permutation is the number of ways to arrange things. Eg: Password is 2045 (order matters) It is denoted by P(n, r) and given by P(n, r) =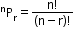, where 0 ≤ r ≤ n n →  number of things to choose from r → number of things we choose ! → factorial

   Combination is the number of ways to choose things.Eg: A cake contains chocolates, biscuits, oranges and cookies. (Order does not matter) It is denoted by C(n, r) and given by C(n, r) =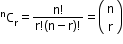, where 0 ≤ r ≤  n →  number of things to choose from r →  number of things we choose ! →  factorial

2. Permutation
   If n is the number of distinct things and r things are chosen at a time.
   i. Permutation of objects when all are not distinct:
      Permutation =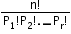 , 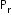→ Number of things among ‘n’ which are alike of rth type.
   ii. Circular permutation
   
   1. When clockwise and anti-clockwise arrangements are different:
       Number of permutations: (n - 1)!
   2. When clockwise and anti-clockwise arrangements are the same:
       Number of permutations: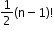 
   iii. Permutation under restrictions
        Selecting and arranging r distinct objects from n

1.  When ‘k’ particular things are always to be included.
   Number of permutations: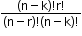
   
2. When a particular thing is always to be included (k = 1).
   Number of permutations: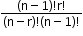
   
3. When ‘k’ particular things are never included.
   Number of permutations: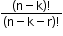
   
4.  When a particular thing is never included.
   Number of permutations: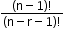
   
5. When ‘l’ particular things always come together.
   Number of permutations: (n - l + 1)! ⨯ l!
6. When ‘l’ particular things never come together.
   Number of permutations: n! - (n - l + 1)! ⨯ l!

i. Permutations with repetition Number of permutations: nPr= nr (Repetition, order matters)     Out of          ←  Taking 2 at a time

ii.  Permutations without repetition 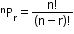(No repetition, order matters) Out of              ←  Taking 2 at a time

3.Combination

i Total number of combinations Ways of selecting one or more things at a time. Number of combinations: When ‘k1’ alike objects of one kind, ‘k2’ alike objects of the second kind … ‘kn’ alike objects of the nth kind. Number of combinations: When ‘k1’ alike objects of one kind, ‘k2’ alike objects of the second kind … ‘kn’ alike objects of the nth kind and rest ‘p’ elements are different. Number of combinations:
ii  Combinations under restriction When ‘k’ particular things are always to be included Number of combinations:  When a particular thing is always to be included (k = 1) Number of combinations: When ‘k’ particular things are never included Number of combinations: When ‘k’ particular things never come together Number of combinations:
i. Combination with repetition   Formula: 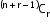 (Repetition, order does not matter)   Out of     ← Taking 2 at a time	ii. Combination without repetition   Formula: 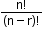   (No repetition, order does not matter)   Out of     ←Taking 2 at a time