Co-ordinate Geometry
Co-ordinate Geometry PDF Notes, Important Questions and Synopsis
SYNOPSIS
Coordinate Geometry
Coordination of Algebra and Geometry is called coordinate geometry.
- Cartesian Coordinate System:
XOX’ and YOY’ are coordinate axes.
The axes divide the coordinate system into four regions called quadrants.
x y 1st quadrant + + 2nd quadrant - + 3rd quadrant - - 4th quadrant + - - Lattice point: A point whose abscissa and ordinate are integers.
-
Distance between two points P(x1, y1) and Q(x2, y2) is given by
PQ =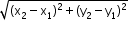
-
Coordinates of different centres of a Triangle:
- Centroid:
The point of concurrency (intersection) of the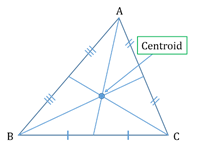
medians of a triangle. - In-centre:
The point of concurrency (intersection) of the internal bisectors of the angles of a triangle.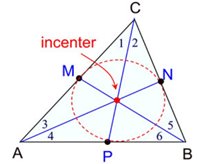
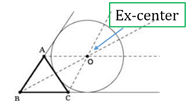
- Ex-centre:
The point at which the bisector of one interior angle meets the lines bisecting the two external angles of the opposite side.
- Circumcentre:
A point which is equidistant from all the three vertices of a triangle.

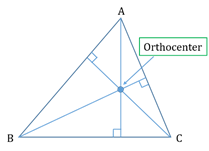
- Orthocentre:
The point of concurrency (intersection) of the altitudes of a triangle.
- Centroid:
-
Locus and its equation:
i. Locus is the curve described by a point which moves under the given condition(s).
ii. Equation of the locus of a point is the relation which is satisfied by the coordinates of every point on the locus of the point. -
Polar coordinates:
Polar coordinates express the location of a point as (r, Ө), where
r → the distance of a point from the origin
Ө → the angle from the positive x-axis to the point -
Shifting of origin:
Shifting the origin to another point by drawing two lines, one
parallel to the x-axis and another parallel to the y-axis is the translation of axes.
Intersection of two lines drawn is the origin for the new coordinate system or of translation.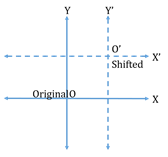
-
Rotation of Axes:
In the rotation of axes, the origin is kept fixed whereas the X and Y
axes are to be rotated to obtain the new coordinate axes X’ and Y’.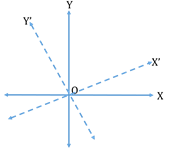
-
Slope of a line:
The angle made by the line with the positive direction of the x-axis
and measured anticlockwise is called the inclination of the line.
The trigonometric tangent of this angle is called the slope (gradient) of the line.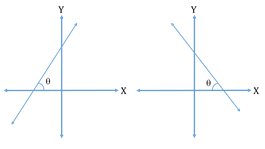
-
Collinearity of Three points:
Three points A, B and C are collinear if the slope of line AB is equal to the slope of line BC. -
Angle between two lines:
Straight Lines
If two lines L1 and L2 are parallel, then the angle between them is 0°.
If two lines L1 and L2 are perpendicular, then the angle between them is 90°. - A line parallel to the y-axis will be of the form x = a, where ‘a’ is the distance between the line and y-axis.
-
A line parallel to the x-axis will be of the form y = b, where ‘b’ is the distance between the line and x-axis.
-
Intercepts of a line:
If a line L cuts the x-axis at point A(a, 0) and the y-axis at point B(0, b), then a and b are its x-intercept and y-intercept, respectively. -
Concurrency of three lines:
Three lines are said to be concurrent if they pass through a common point (meet at only one point). -
Family of Straight Lines:
Set of infinite straight lines which pass through (intersect at) a single point A. -
General form of the second degree equation in x and y:
General form of second degree equation in x and y is given by
ax2 + 2hxy + by2 +2gx + 2fy + c = 0 -
Homogeneous equation of nth degree:
An equation (whose RHS is zero) in which the sum of the powers of x and y in every term is the same (say n) is called a homogeneous equation of nth degree.
Circle
- Circle is a locus of a point which moves in a plane such that its distance from a fixed point is always constant.
A fixed point is the centre of the circle. - Parts of a Circle:

- Circumference:
Length of the boundary or outer edge of the circle. - Radius:
Length of a line from the centre to the edge of the circle. - Diameter:
Length of a line which passes through the centre with its endpoints lying on the circle. - Chord:
A straight line joining any two points lying on
the circumference of a circle. -
Arc:
A part of the circumference of a circle. -
Sector:
The area which is enclosed by an arc and the two radii of a circle. -
Segment:
The area inside a circle which is enclosed by an arc and the chord. -
Tangent:
A straight line which touches the circle at a point.
- Circumference:
- Normal to a Circle
The normal of a circle at any point is a straight line which is perpendicular to the tangent at the point of contact.
Note: Normal of the circle always passes through the centre of the circle. -
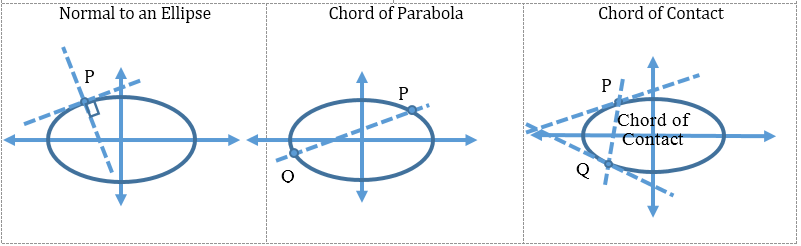
Chord of Contact
From any external point A, draw a pair of tangents touching the circle at points P and Q.
Then, PQ is the chord of contact with P and Q as its points of contact.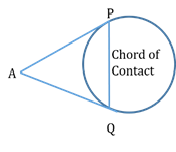
-
Director Circle of a Circle:
The locus of the point of intersection of two perpendicular tangents to a given circle is called its director circle.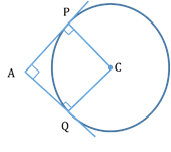
-
Angle of Intersection of two Circles:
Angle between two circles is defined as the angle between the tangents of the two circles at the point of intersection.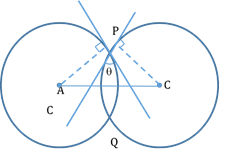
-
Orthogonal Circles:
If the angle between the circles is 90°, then the circles are said to be orthogonal circles.
We can also say that they cut each other orthogonally. -
Radical Axis:
Radical axis of two circles is the locus of the point which moves such that the lengths of the tangents drawn from it to the two circles are equal. -
Radical centre:
Point at which the radical axes of three circles taken in pairs meet. -
Common chord:
Chord joining the points of intersection of two circles.
Parabola
The section obtained by the intersection of a plane with a cone is called a conic section
- Parabola:
A symmetrical open plane curve obtained by the intersection of a cone with a plane parallel to its side (base).
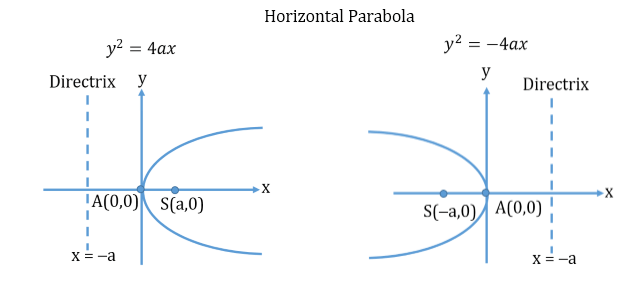
General Equation of a parabola: y2=4ax
- Recognising conics:
General equation of conics: ax2+2hxy+by2+2gx+2fy+c=0
Δ=abc+2fgh-af2-bg2-ch2
Condition
- Δ≠ 0, h = 0, a = b
- Δ≠ 0, ab - h2 = 0
- Δ≠ 0, ab - h2 > 0
- Δ≠ 0, ab - h2 < 0
- Δ≠ 0, ab - h2 < 0 and a + b = 0
Nature of Conics
- Circle
- Parabola
- Ellipse or empty set
- Hyperbola
- Rectangular hyperbola
- Parameters of a parabola:
- Vertex: (0, 0)
- Axis: y = 0 (X-axis)
- Focal Distance:
Distance of a point on the parabola from the focus. - Double Ordinate:
A chord which is perpendicular to the axis of symmetry.
- Focus: (a, 0)
- Directrix: x = -a
- Focal Chord:
A chord which passes through the focus. - Latus Rectum:
Double ordinate passing through the
focus.
Length of the latus rectum is 4a.
- Vertex: (0, 0)
- Types of Parabola:
- Tangent, Normal and Chord to a Parabola
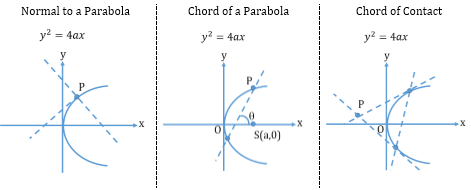
- Reflection Property of a Parabola:
The tangent at any point P to a parabola bisects the distance between the focal chord through P and the perpendicular from P to the directrix.
Ellipse
- Ellipse:
- Ellipse is the set of all points in a plane, the sum of whose distances from two fixed points in the plane is a constant
- The two fixed points are called the foci of the ellipse.
- The midpoint of the line joining the two foci is called the centre of the ellipse.
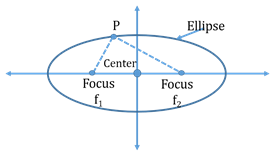
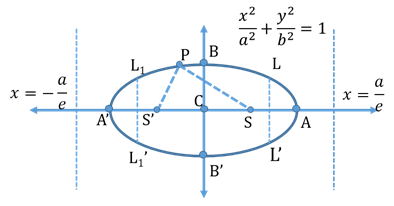
- Parameters of an Ellipse
- Vertices are A and A’
- Directrices:
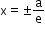
- Focal chord: A chord which passes through a focus.
- Minor axis: BB’
- Focal Radii: SP and S’P
- Focal distance: Sum of the focal radii of any point is equal to the length of the major axis.
- Major axis: AA’
- Eccentricity:e=
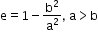
- Double ordinate: A chord perpendicular to the major axis.
- Latus Rectum: Length =
-
Auxiliary Circle and Eccentric angle:
A circle described on the major axis as a diameter is called the Auxiliary circle.
Equation of Auxiliary circle: x2+y2=a2
Take two points P and Q on the ellipse and auxiliary circle respectively, such that the x-coordinate is the same for both points.
Here, Ө is called the eccentric angle of point P.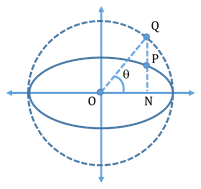
- Tangent, normal and chord of an ellipse:
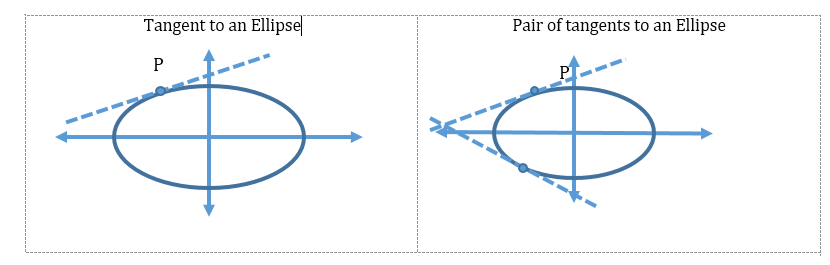
-
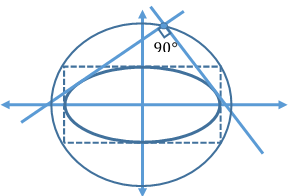
Director Circle of an Ellipse:
Locus of the point of intersection of the tangents which meet at right angles is called the Director circle.
The Director circle is given as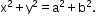
Hyperbola
- Hyperbola
A hyperbola is the set of all points, the difference of whose distance from two fixed points is constant.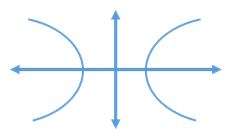
- Parameters of a Hyperbola:
- Foci: The two fixed points are called the foci of the Hyperbola.
- Transverse axis: The line through the foci.
- Eccentricity:
(e) =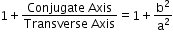
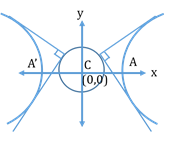
- Vertices: The points at which the hyperbola intersects the transverse axis.
A(a, 0) and A’(-a, 0) - Foci S = (ae, 0) and S’ = (-ae, 0)
- Centre (C): The midpoint of the line joining the foci.
- Conjugate axis: The line through the centre and perpendicular to the Transverse axis.
- Focal distance: Distance of any point on the hyperbola from the foci.
|PS - PS’| = 2a and Focal length SS’ = 2ae - Distance between foci = 2c
- Equations of Directrices:
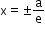
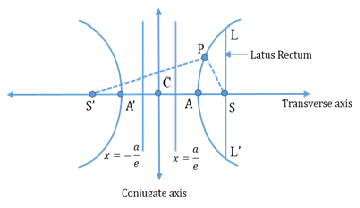
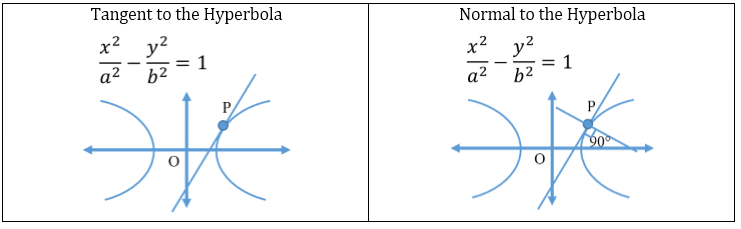
- Tangent and Normal to the Hyperbola:
- Director Circle of a Hyperbola:
Locus of the point of intersection of tangents which are at right angles is called the director circle.
It is given by
-
Conjugate Hyperbola:
For a hyperbola, there exist a hyperbola such that the conjugate and transverse axes of one is equal to the conjugate and transverse axes of the other.Such hyperbolas are known as conjugate to each other.
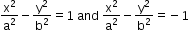
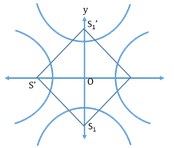
- Rectangular (equilateral) hyperbola:
The length of the transverse and conjugate axis are equal for a Rectangular hyperbola.
- Vertices: (c, c) & (-c, -c)
- Directrices: x + y = ±
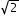
- Foci:
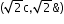
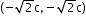
- Latus Rectum: ℓ = 2
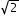 c
c - Eccentricity: e =
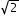
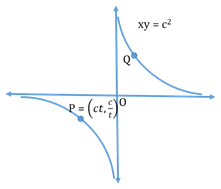
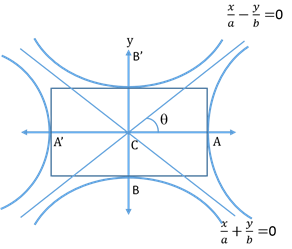
- Asymptotes of Hyperbola:
-
Asymptotes are the lines which get closer and closer to the curve but never touch the curve.
-
When we combine the equation of asymptotes, it gives
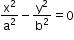
-
So, the equation of a pair of asymptotes differ with a hyperbola and conjugate hyperbola by the same constant only.
-
Asymptotes are the tangents to hyperbola with the centre at infinity.
-
They pass through the centre of the hyperbola and the bisectors of angles between them are the axes of the hyperbola.
-
-
Auxiliary Circle and eccentric angle:
A circle drawn with centre C and diameter as transverse axis is called the auxiliary circle of the hyperbola.
Its equation is x2+y2=a2
θ is the eccentric angle of the point P on the hyperbola.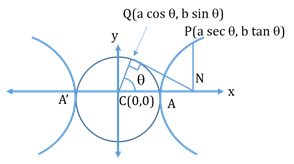
![]()
Related Chapters
- Sets, Relations and Functions
- Complex Numbers and Quadratic Equations
- Matrices and Determinants
- Permutations and Combinations
- Mathematical Induction
- Binomial Theorem and its Simple Applications
- Sequences and Series
- Limit, Continuity and Differentiability
- Integral Calculus
- Differential Equations
- Three Dimensional Geometry
- Vector Algebra
- Statistics and Probability
- Trigonometry
- Mathematical Reasoning