Vector Algebra
Vector Algebra PDF Notes, Important Questions and Synopsis
SYNOPSIS
Vector Algebra
- Vector is a quantity having both magnitude and direction.
Note: A directed line segment is a vector denoted by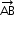 or simply
or simply 
where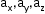 denotes ith, jth, kth components.
denotes ith, jth, kth components. - Magnitude of a vector
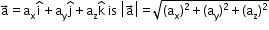
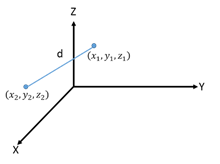
- Distance between 2 points in 3D plane is given by
d = |PQ| =
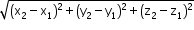
-
Internal/External division:
- Internal division
Let P and Q be the two given points. Let be the point which divides PQ internally in the ratio m : n.
be the point which divides PQ internally in the ratio m : n.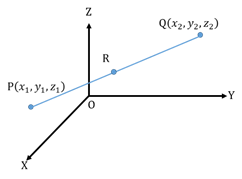
Then its coordinates are
R =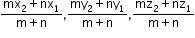
- External Division
Let P and Q be the two given points. Let be the point which divides PQ internally in the ratio m : n.
be the point which divides PQ internally in the ratio m : n.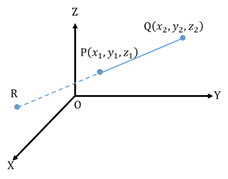
Then its coordinates are
R =
- Internal division
- Types of Vectors:
- Zero Vector:
A vector having zero magnitude, i.e.
if =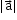 0. Also, it has no direction.
0. Also, it has no direction. - Co-initial vectors:
Two or more vectors having the same initial point. - Collinear Vectors:
Vectors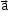 and
and 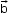 are said to be collinear if they are parallel to each other.
are said to be collinear if they are parallel to each other. - Free vectors:
Vectors whose initial points are not specified.
- Unit Vector:
A vector whose magnitude is 1, i.e. if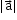 = 1. It is denoted by
= 1. It is denoted by  .
. - Equal vectors:
Vectors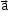 and
and 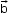 are equal if &
are equal if & 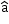 =
=  .
. - Coplanar vectors:
Vectors which are parallel or lying in the same plane are coplanar. - Localised vectors:
Vectors drawn parallel to a given vector, but through a specified point as the initial point.
Position vector: A vector 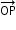 having O and P as its initial and terminal points, is called the position vector of point P, where O is the origin.
having O and P as its initial and terminal points, is called the position vector of point P, where O is the origin. - Zero Vector:
- Operations on vectors:
i. Addition of vectors:
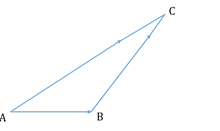
A, B and C are three points, then
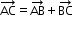 .
.
This is known as the triangle law of vector addition.
Also, if we have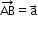 &
&  , then
, then
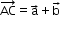
 ii. Multiplication of a vector by a scalar:Let
ii. Multiplication of a vector by a scalar:Let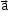 be the vector and k be a scalar. Product of
be the vector and k be a scalar. Product of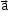 and k is
and k is 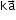 , where each component of
, where each component of 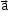 is multiplied by k.
is multiplied by k.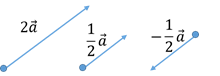
- Linear combination/dependence/independence
- Linear Combination:
A vector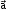 is said to be a linear combination of vectors
is said to be a linear combination of vectors 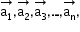 if there exist scalars such that
if there exist scalars such that
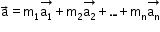 .
. - Linearly Independent:
A system of vectors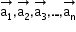 is said to be linearly independent if for
is said to be linearly independent if for 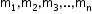 such that
such that 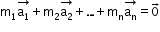
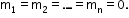
- Linearly Dependent:
A system of vectors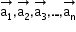 are said to be linearly dependent if there exist scalars
are said to be linearly dependent if there exist scalars 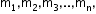
not all zero, such that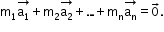
- Linear Combination:
- Vector Lines:
To determine vector equation of a line, we need
i. A point on the line
ii. A vector parallel to the line - Vector Planes:To determine vector equation of a plane, we need
- A point on the plane
- A vector perpendicular to the line
-
Scalar or dot product of vectors:
Scalar product of vectors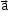 and
and 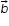 is the projection of
is the projection of 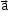 over
over 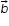 .
.
Denoted by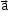 .
.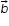 and given by
and given by 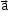 .
. 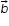 =
= 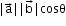
-
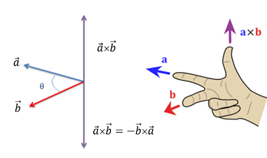
Vector or cross product of vectors:
Vector product of vectors and
and  is written as
is written as  and it is defined as
and it is defined as sinθ
sinθ 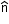 , where n ̂ is a unit vector
, where n ̂ is a unit vector
along the line perpendicular to both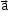 and
and 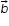 .
.
-
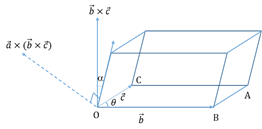
Scalar triple product:
The dot product of one of the vectors with the cross product of the other two.
i.e. Scalar triple product of three vectors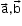 and
and 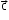 is
is 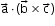 .
.
It represents the volume of the parallelepiped.
Also, the volume of a tetrahedron is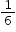 th times the volume of the parallelepiped.
th times the volume of the parallelepiped.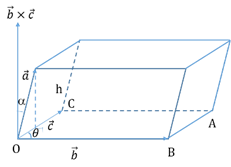
-
Vector triple product:
Vector triple product of three vectors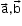 and
and 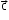 is the vector
is the vector 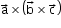
Related Chapters
- Sets, Relations and Functions
- Complex Numbers and Quadratic Equations
- Matrices and Determinants
- Permutations and Combinations
- Mathematical Induction
- Binomial Theorem and its Simple Applications
- Sequences and Series
- Limit, Continuity and Differentiability
- Integral Calculus
- Differential Equations
- Co-ordinate Geometry
- Three Dimensional Geometry
- Statistics and Probability
- Trigonometry
- Mathematical Reasoning