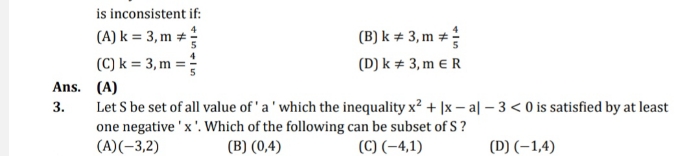Limit, Continuity and Differentiability
Limit, Continuity and Differentiability PDF Notes, Important Questions and Synopsis
SYNOPSIS
- The expected value of the function as dictated by the points to the left of a given point defines the left-hand limit of the function at that point. The limit
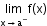 is the expected value of ‘f’ at x = a, given the values of ‘f’ near ‘x’ to the left of ‘a’.
is the expected value of ‘f’ at x = a, given the values of ‘f’ near ‘x’ to the left of ‘a’. -
The expected value of the function as dictated by the points to the right of a given point defines the right-hand limit of the function at that point. The limit
 is the expected value of ‘f’
is the expected value of ‘f’
at x = a, given the values of ‘f’ near ‘x’ to the right of ‘a’. -
Let y = f(x) be a function. Suppose that ‘a’ and ‘L’ are numbers such that as ‘x’ gets closer and closer to ‘a’, f(x) gets closer and closer to ‘L’. We say that the limit of f(x) at x = a is L,
i.e.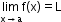
-
Limit of a function at a point is the common value of the left- and right-hand limit if they coincide,
i.e. if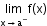 =
=  .
. -
Real-life examples of LHL and RHL:
i. If a car starts from rest and accelerates to 60 km/hr in 8 seconds, which means the initial speed of the car is 0 and it reaches 60 km/hr 8 seconds after the start. On recording the speed of the car, we can see that this sequence of numbers is approaching 60 km in such a way that each member of the sequence is less than 60. This sequence illustrates the concept of approaching a number from the left of that number.
ii. Boiled milk which is at a temperature of 100 degrees is placed on a shelf. The temperature goes on dropping till it reaches room temperature. As the time duration increases, temperature of milk t approaches room temperature, say 30°C .This sequence illustrates the concept of approaching a number from the right of that number. -
Let f and g be two functions such that both
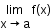 and
and 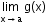 exist, then
exist, then
i. Limit of the sum of two functions is the sum of the limits of the functions,
i.e.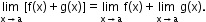
ii. Limit of the difference of two functions is the difference of the limits of the functions,
i.e.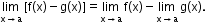
iii. Limit of the product of two functions is the product of the limits of the functions,
i.e.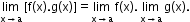
iv. Limit of the quotient of two functions is the quotient of the limits of the functions
(whenever the denominator is non-zero),
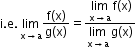
-
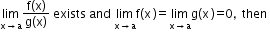

-
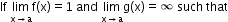
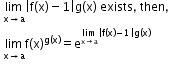
-
For any positive integer n,
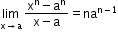
-
Limit of a polynomial function can be computed using substitution or algebra of limits.
-
Methods used to evaluate algebraic limits:
i. Direct substitution
ii. Factorisation
iii. Rationalisation
iv. Using some standard limits
v. Evaluation of algebraic limits at infinity -
Let ‘f’ and ‘g’ be two real-valued functions with the same domain such that f(x) ≤ g(x) for all x in the domain of definition. For some ‘a’, if both
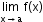 and
and 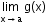 exist, then
exist, then  .
. -
Let f, g and h be real functions such that f(x) ≤ g(x) ≤ h(x) for all x in the common domain of definition. For some real number a, if
 f(x) = ℓ=
f(x) = ℓ=  h(x), then
h(x), then g(x) = ℓ.
g(x) = ℓ. -
14. If ‘f’ is a real-valued function and ‘a’ is a point in its domain of definition, then the derivative of ‘f’ at ‘a’ is defined by
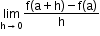
Provided this limit exists and is finite. Derivative of f(x) at ‘a’ is denoted by f’(a). -
A function is differentiable in its domain if it is always possible to draw a unique tangent at every point on the curve.
-
A function f(x) is said to be continuous at a point c if
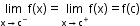
-
A real function f is said to be continuous if it is continuous at every point in the domain of f.
-
If f and g are real-valued functions such that (f o g) is defined at c, then
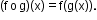
If g is continuous at c and if f is continuous at g(c), then (f o g) is continuous at c. -
A function f is differentiable at a point c if left-hand derivative (LHD) = right-hand derivative (RHD),
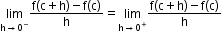
-
If a function f is differentiable at every point in its domain, then
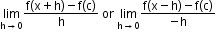 is called the derivative or differentiation of f at x and is
is called the derivative or differentiation of f at x and is
denoted by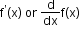 .
. -
If
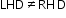 , then the function f(x) is not differentiable at x = c.
, then the function f(x) is not differentiable at x = c. -
Geometrical meaning of differentiability:
The function f(x) is differentiable at a point P if there exists a unique tangent at point P. In other words, f(x) is differentiable at a point P if the curve does not have P as its corner point. -
A function is said to be differentiable in an interval (a, b) if it is differentiable at every point of (a, b).
-
A function is said to be differentiable in an interval [a, b] if it is differentiable at every point of [a, b].
-
Chain rule of differentiation: If f is a composite function of two functions u and v such that f = v(t) and t = u(x), also both
 exist, then
exist, then 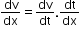 .
. -
Logarithm of a to the base b is x, i.e. logba = x if bx = a, where b > 1 is a real number.
-
Functions of the form x = f(t) and y = g(t) are parametric functions.
-
Rolle’s theorem: If f : [a, b] → R is continuous on [a, b] and differentiable on (a, b) such that f(a) =
f(b), then there exists some c in (a, b) such that f’(c) = 0. -
Mean-value theorem: If f : [a, b] → R is continuous on [a, b] and differentiable on (a, b), then there
exists some c in (a, b) such that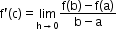 .
. -
A function is continuous at x = c if the function is defined at x = c and the value of the function at x = c equals the limit of the function at x = c.
-
If function f is not continuous at c, then f is discontinuous at c and c is called the point of discontinuity of f.
-
Every polynomial function is continuous.
-
The greatest integer function [x] is not continuous at the integral values of x.
-
Every rational function is continuous.
-
Algebra of continuous functions
i. Let f and g be two real functions continuous at a real number c, then
f + g is continuous at x = c.
ii. f - g is continuous at x = c.
iii. f . g is continuous at x = c.
iv.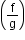 is continuous at x = c, [provided g(c) ≠ 0]
is continuous at x = c, [provided g(c) ≠ 0]
v. kf is continuous at x = c, where k is a constant. -
Consider the following functions:
i. Constant function
ii. Identity function
iii. Polynomial function
iv. Modulus function
v. Exponential function
vi. Sine and cosine functions
These functions are continuous everywhere. -
Consider the following functions:
i. Logarithmic function
ii. Rational function
iii. Tangent, cotangent, secant and cosecant functions
These functions are continuous in their domains. -
If f is a continuous function, then
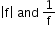 are continuous in their domains.
are continuous in their domains. -
Inverse functions
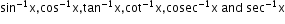 are continuous functions in their respective domains.
are continuous functions in their respective domains. -
The derivative of a function f with respect to x is f’(x) which is given by
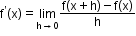 .
. -
If a function f is differentiable at a point c, then it is also continuous at that point.
-
Every differentiable function is continuous, but the converse is not true.
-
Every polynomial function is differentiable at each
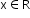 .
. -
Every constant function is differentiable at each
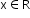 .
. -
The chain rule is used to differentiate composites of functions.
-
The derivative of an even function is an odd function and that of an odd function is an even function.
-
Algebra of derivatives:
If u and v are two functions which are differentiable, then
i.
ii.
iii.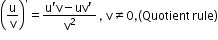
-
Implicit functions:
If it is not possible to separate the variables x and y, then the function f is known as an implicit function. -
Exponential function: A function of the form y = f(x) = bx, where base b > 1.
i. Domain of the exponential function is R, the set of all real numbers.
ii. The point (0, 1) is always on the graph of the exponential function.
iii. The exponential function is ever increasing. -
The exponential function is differentiable at each
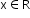 .
. -
Properties of logarithmic functions:
i. Domain of log function is R+.
ii. The log function is ever increasing.
iii. For ‘x’ very near to zero, the value of log x can be made lesser than any given real number. -
Logarithmic differentiation is a powerful technique to differentiate functions of the form f(x) = [u(x)]v(x). Here, both f(x) and u(x) need to be positive.
-
To find the derivative of a product of a number of functions or a quotient of a number of functions, take the logarithm of both sides first and then differentiate.
-
Logarithmic differentiation:
y = ax
Taking logarithm on both sides,
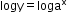
Using the property of logarithms,
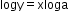
Now differentiating the implicit function,
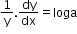
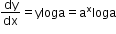
-
The logarithmic function is differentiable at each point in its domain.
-
Trigonometric and inverse-trigonometric functions are differentiable in their respective domains.
-
The sum, difference, product and quotient of two differentiable functions are differentiable.
-
The composition of a differentiable function is a differentiable function.
-
A relation between variables x and y expressed in the form x = f(t) and y = g(t) is the parametric form with t as the parameter. Parametric equation of parabola y2 = 4ax is x = at2, y = 2at.
-
Differentiation of an infinite series: If f(x) is a function of an infinite series, then to differentiate the function f(x), use the fact that an infinite series remains unaltered even after the deletion of a term.
-
Parametric differentiation:
Differentiation of the functions of the form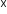 = f(t) and y = g(t):
= f(t) and y = g(t): 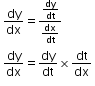
-
Let u = f(x) and v = g(x) be two functions of x. Hence, to find the derivative of f(x) with respect g(x), we use the following formula:
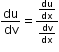
-
If y = f(x) and
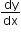 = f’(x) and if f’(x) is differentiable, then
= f’(x) and if f’(x) is differentiable, then 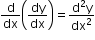 or f’’(x) is the second-order derivative of y with respect to x.
or f’’(x) is the second-order derivative of y with respect to x. -
If x = f(t) and y = g(t), then
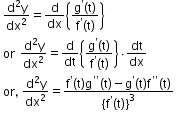
Related Chapters
- Sets, Relations and Functions
- Complex Numbers and Quadratic Equations
- Matrices and Determinants
- Permutations and Combinations
- Mathematical Induction
- Binomial Theorem and its Simple Applications
- Sequences and Series
- Integral Calculus
- Differential Equations
- Co-ordinate Geometry
- Three Dimensional Geometry
- Vector Algebra
- Statistics and Probability
- Trigonometry
- Mathematical Reasoning