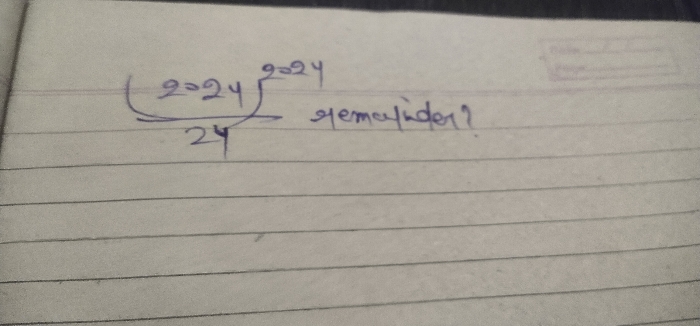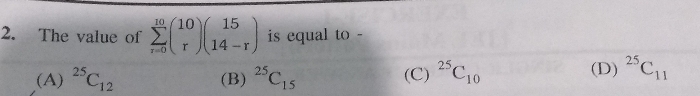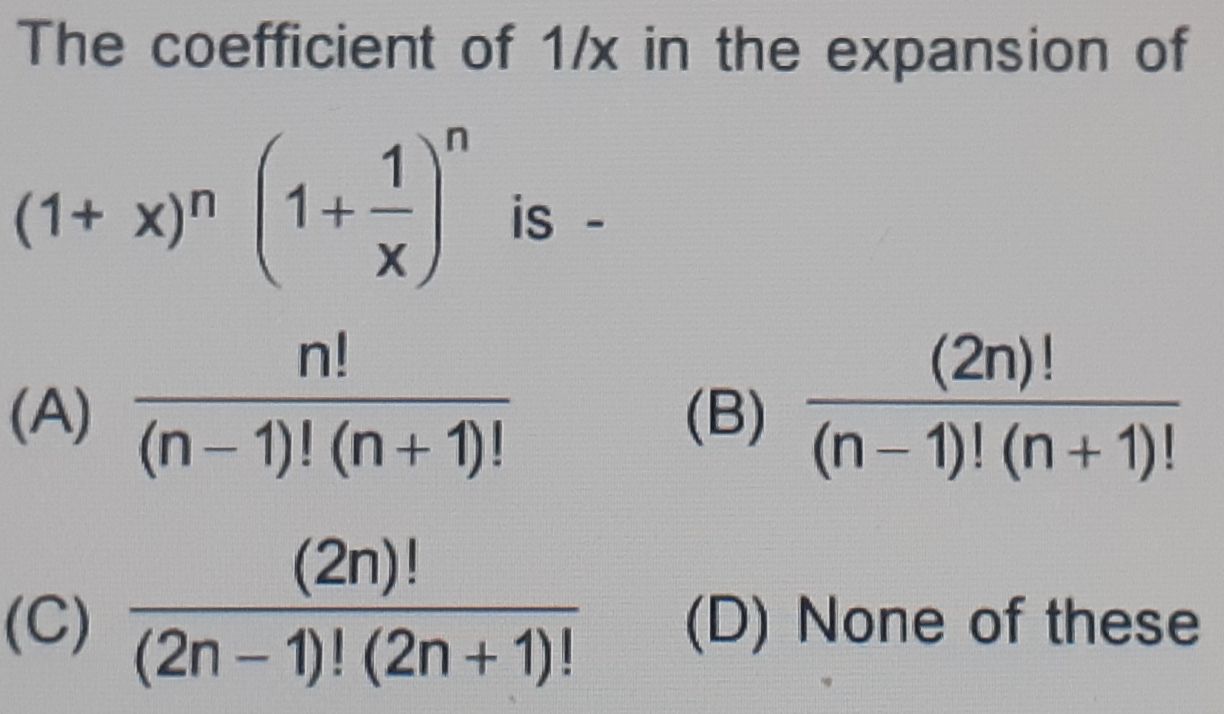Binomial Theorem and its Simple Applications

SYNOPSIS

1. A binomial is a polynomial having only two terms. For e.g 2y²- 1
2. (x + y)ⁿ can be expanded using the Binomial theorem without actually multiplying it n times.
   

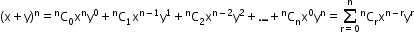
3. Properties of Binomial Expansion (x + y)ⁿ

   i.Total number of terms in this expansion is n + 1.

   ii.The exponent of x decreases by 1, while the exponent of y increases by 1 in subsequent terms.

   iii.The first term is   and the final/last term is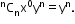  

   iv.The general term in this expansion is given by
    

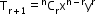
4. Binomial Coefficients:
   Binomial coefficients in the expansion of (x + y)ⁿ are simply the number of ways of choosing x from the brackets and y from the rest.

5. Pascal’s Triangle:
   Binomial coefficients can be found using Pascal’s triangle given below.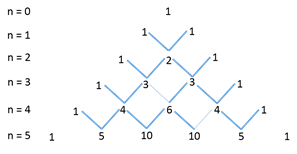
   
   We can also say that
   .
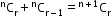   Also, the binomial coefficient is given by 
    

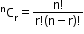
6. Terms in the binomial expansion of (x + y)n

   
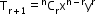
   i.General Term (r^th term): General term in the expansion of (x + y)ⁿ is given by

   ii.Middle Term(s):

      1. When n is even,
          

     2. When n is odd,
        and 
   
   iii.Greatest Term:
   In any binomial expansion, the values of the terms increase, reach a maximum and then decrease.
   
   So, to find the greatest term, find the value of r till  
   
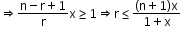
   So, the greatest term occurs when
   r =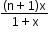 
   iv.Term independent of x:
   

   The term independent of x is the term not containing x.
   So, find the value of r such that the exponent of x is zero.

7. Applications of Binomial Expansion:
   i. We have a very important result
   
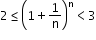      , n ≥ 1, n ∊ N
   ii. Finding the remainder using Binomial Theorem:
   To find the remainder when pn is divided by q, adjust the power of p to p^m which is very close to b, say with difference 1 and then divide by taking the remainder always positive.