NCERT Solutions for Class 9 Maths CBSE
Discover a collection of all the necessary items required for studying class 9 Maths.
CBSE Class 9 syllabus is extensive, especially. Acing Maths requires perseverance and students often struggle to find solutions for their queries. In order to ease the stress, we have come up with these solutions you can find the answer and step-wise solution to each and every question from NCERT for CBSE Class 9 Maths exam.
Use the class 9th maths ncert solutions to study the entire syllabus of Maths. Solutions or extra practice questions for the syllabus are a a constant need and we cater efficiently to that need with our study material.
NCERT for CBSE Class 9 Maths provides chapter-wise solutions with elaborate explanations. Concepts are explained in detail with accurate NCERT Solutions for each chapter. These solutions have been formulated by subject experts. CBSE students can refer to the detailed chapter-wise solutions, which provide answers to all your queries. NCERT solutions for class 9 Maths is a must-have to improve your progress and ace your scores. Access to these solutions is quick and hassle-free.
TopperLearning offers a wholesome target oriented package of NCERT solutions for Class 9 Maths. Gain access to 400+ Video Lectures, 200+ Revision Notes, 12,000+ Question Banks, and CBSE sample paper class 9 with solutions that are completely adequate for preparation.
Apart from NCERT Solutions for Class 9 Maths, TopperLearning offers many add-on materials that will ace a student’s score. CBSE sample papers are designed by our Maths Subject Experts and the papers are consistent with the latest syllabus.
We also provide CBSE Class 9 Maths revision notes for a quick brush up. Here is the list of all the chapters from the syllabus, Click on the chapter and excel in learn CBSE Class 9 Maths.
Chapter-wise list of NCERT solution for Class 9 Maths
- Chapter 1 - Number Systems
- Chapter 2 - Polynomials
- Chapter 3 - Coordinate Geometry
- Chapter 4 - Linear Equations in Two Variables
- Chapter 5 - Introduction to Euclid's Geometry
- Chapter 6 - Lines And Angles
- Chapter 7 - Triangles
- Chapter 8 - Quadrilaterals
- Chapter 9 - Circles
- Chapter 10 - Heron's Formula
- Chapter 11 - Surface Areas and Volumes
- Chapter 12 - Statistics
NCERT Solutions for Class 9 Maths
NCERT Solutions for Class 9 Maths Chapter 1 Number System
This chapter briefly takes into account the conceptual knowledge of a student from previous grades. The student will have an in-depth understanding of the real number system by performing various operations on it. It will also involve revision of rational and irrational numbers along with natural numbers, whole numbers, and integers. The use of number line enables a prim and proper understanding that builds a strong foundation of CBSE Class 9 Maths
These basic concepts lead to decimal expansion and rationalisation. The student will be able to find out whether the given decimal is non-terminating repeating or terminating and will be able to rationalise the irrational numbers with TopperLearning’s NCERT solutions for Class 9 Maths.
The chapter has six exercises as mentioned below. Each question is solved with an apt approach by our subject experts. The solutions are self-explanatory and provide complete clarity.
The numbers which can be represented in the form of p/q, where q ≠ o and p and q are integers are called rational numbers. Rational numbers are denoted by Q. If p and q are co-prime then the rational number is in its simplest form. All-natural numbers, whole numbers and integer are rational number. Equivalent rational numbers (or fractions) have same (equal) values when written in the simplest form. Rational number between two numbers x and y = x+y/2 .
There are infinitely many rational numbers between any two given rational numbers. The numbers which are not of the form of p/q, where q ≠ 0 and p and q are integers are called irrational numbers. For example: √2, √7, 𝛑 etc. Rational and irrational numbers together constitute are called real numbers. The collection of real numbers is denoted by R.
Irrational number between two numbers x and y

Chapter 1 - Number Systems Exercise Ex. 1.1
There are four questions in this exercise. This exercise can also be called a recap of previous knowledge, with some new concepts. Students should be able to list the rational numbers between any two natural numbers. Our subject experts have solved these questions in an elaborate manner. Students can tally their solutions and use our doubt solver "Ask a Doubt" feature in case of doubts.
Chapter 1 - Number Systems Exercise Ex. 1.2
Irrational numbers is a tricky concept to comprehend. TopperLearning makes it simpler for all students by solving all four questions in this exercise. These questions are about understanding the scope of different types of numbers and playing the irrational numbers on the number line. Each solution has a concept insight, which makes it simpler to learn CBSE Class 9 Maths. Check your solutions and use our doubt solver "Ask a Doubt" feature in case of doubts.
Chapter 1 - Number Systems Exercise Ex. 1.3
The focus in this exercise is on rational and irrational numbers along with decimal expansion. The process of representation of real numbers on the number line using their decimal expansions is thoroughly discussed. This exercise has nine questions with some sub-questions as well. Our subject experts have not only provided with the solutions but have also given you a concept insight for understanding why and how the answer is obtained. Students will be more familiar and shall be able to distinguish between rationals and irrationals with TopperLearning’s class 9th maths ncert solutions. Use our doubt solver "Ask a Doubt" feature and get your queries resolved.
Chapter 1 - Number Systems Exercise Ex. 1.4
This part focuses on the process of successive magnification and how real numbers are placed on the number line using successive magnification. There are only two questions in this exercise. A stepwise approach is best for making a Class 9 Maths student understand this concept. Our subject experts have used the same technique to provide you with the solutions.
Chapter 1 - Number Systems Exercise Ex. 1.5
This exercise targets performing different operations on real numbers to infer if they follow the basic laws of Maths. The reference of these properties and operations lays the ground base of understanding advanced academic Maths. This exercise comprises 5 questions with some sub-questions. Our subject experts understand what may puzzle the students and hence with each solution, there is a reason or property associated to provide clarity. Our experts will help you with your doubts with our doubt solver "Ask a Doubt".
Chapter 1 - Number Systems Exercise Ex. 1.6
The concept of Laws of Exponents from the lower grades is revised in this exercise. The operation of laws of exponents on real numbers is analysed and assessed with only three questions and some sub-questions. Each of these questions is solved in an elaborated manner accompanied by some formulae from the previous grades for quick revision. This is the last exercise of this chapter after which the student shall have a thorough foundation of the number system.
NCERT Number Systems Class 9 Videos
NCERT Number Systems Class 9 Revision Notes
NCERT Number Systems Class 9 Most Important Questions
NCERT Number Systems Class 9 MCQ
NCERT Number Systems Class 9 FIB
NCERT Number Systems Class 9 Short Answer Questions
List of sub chapters
Class 9 Maths- Rational numbers
Class 9 Maths- Irrational numbers
Class 9 Maths- Laws of exponents
Class 9 Maths- Representation on number line
This indeed is a great kick start for the CBSE syllabus for class 9 Maths. Get your doubts quickly resolved using our doubt solver "Ask a Doubt".
NCERT Solutions for Class 9 Maths Chapter 2 Polynomials
NCERT Solutions for Class 9 Maths Chapter 3 Coordinate Geometry
This chapter recaps your basics about algebraic expressions. Polynomial is a specific type of algebraic expression and so this chapter involves all the terminologies and various operations on it. Our video solutions will be an excellent resort for this chapter from CBSE Class 9 Maths.
A polynomialp(x) in one variable x is an algebraic expression in x of the form
p(x) = anxn + an-1xn-1 + an-2xn-2 + ...... + a2x2 + a1x + a0, where
a0,a1, a2.......an are constants
x is a variable
a0,a1, a2.......an are respectively the coefficients of xi
Each of anxn + an-1xn-1 + an-2xn-2 + ...... + a2x2, a1x, a0 with an ≠ is called a term of a polynomial.
Division algorithm
If p(x) and g(x) are the two polynomials such that degree of p(x) ≥ degree of g(x) and g(x) ≠ 0, then we can find polynomials q(x) and r(x) such that:
p (x) = g(x) q(x) + r(x)
where, r(x) =0 or degree of r(x) < degree of g(x).
Remainder theorem
Let p(x) be any polynomial of degree greater than or equal to one and let a be any real number. If p(x) is divided by the linear polynomial (x – a), then remainder is p(a).
If the polynomial p(x) is divided by (x + a), the remainder is given by the value of p(-a).
Factor theorem
Let p(x) is a polynomial of degree n ≥ 1 and a is any real number such that p(a) = 0, then (x - a) is a factor of p(x).
Converse of factor theorem
Let p(x) is a polynomial of degree n ≥ 1 and a is any real number. If (x - a) is a factor of p(x), then .... p(a) = 0.
An algebraic identity is an algebraic equation which is true for all values of the variables occurring in it.
Some useful quadratic identities:
(x + y)2 = x2 + 2xy + y2
(x - y)2 = x2 - 2xy + y2
(x - y)(x + y) = x2 - y2
(x + a)(x + b) = x2 + (a + b)x + ab
(x + y + z)2 = x2 + y2 + z2 + 2xy + 2yz + 2zx
Here x, y, z are variables and a, b are constants.
Some useful cubic identities:
(x + y)3 = x3 + y3 + 3xy(x + y)
(x - y)3 = x3 - y3 - 3xy(x - y)
x3 + y3 = (x + y)(x2 - xy + y2)
x3 - y3 = (x - y)(x2 + xy + y2)
x3 + y3 + z3 - 3xyz = (x + y + z)(x2 + y2+ z2 - xy - yz - zx)
If x + y + z = 0 then x3 + y3 + z3 = 3xyz
Here, x, y and z are variables.
This chapter is known to have vital importance for high order thinking problems. Our solved CBSE sample paper class 9 and the marking scheme for the questions will help you to understand them. This chapter has five exercises and you can always ask your doubts using our doubt solver "Ask a Doubt" feature where we are available for you round the clock.
Chapter 2 - Polynomials Exercise Ex. 2.1
This exercise gives a basic kick start to understand the concept of Polynomials with TopperLearning’s class 9th maths ncert solutions. The questions from this exercise are generally asked as objective questions. The solution to each of the five questions are provided by our subject experts. Many more similar questions are available in our study material along with CBSE sample paper class 9 for deep and extra practice. You can use our doubt solver "Ask a Doubt" feature in case of doubts.
Chapter 2 - Polynomials Exercise Ex. 2.2
Learn to find the value of a polynomial at a given point, verifying zeroes of a polynomial, and finding Zeroes of a polynomial. Use our study material for CBSE Class 9 Maths Polynomials (exercise 2.2 solution. TopperLearning’s audio-video solutions are the best for a stepwise solution. Our doubt solver "Ask a Doubt" provides quick clarification on your doubts.
Chapter 2 - Polynomials Exercise Ex. 2.3
Discover the process of diving polynomials with the Remainder Theorem in Class 9 Maths textbook solution. These questions are often asked for Board exams. Students can also avail the benefit of referring to the most important questions and the questions asked in previous exercises along with detailed solution with TopperLearning’s study material in the form of Class 9 Maths Notes and Class 9 Maths textbook solution. In case if there are any difficulties, use our doubt solver "Ask a Doubt".
Chapter 2 - Polynomials Exercise Ex. 2.4
Dive in deeper for understanding the factorisation process of polynomials with some quirky problems. There are some more questions for assessment available along with revision notes. However, Class 9 Maths Polynomials exercise 2.4 solution for every question is provided in a detailed manner by our subject experts.
Chapter 2 - Polynomials Exercise Ex. 2.5
The final exercise deals with using algebraic identities with polynomials which are solved in Class 9 Maths textbook solution. This is a tricky area for students and also a zone for making trivial mistakes. Considering this, a stepwise approach is made available with NCERT solutions for Class 9 Maths along with a concept insight for perfect clarity to the student. Refer to class 9th maths ncert solutions and ace your preparations. Our doubt solver "Ask a Doubt" feature solves all your queries.
NCERT Polynomials Class 9 Videos
NCERT Polynomials Class 9 Revision Notes
NCERT Polynomials Class 9 Most Important Questions
NCERT Polynomials Class 9 Short Answer Questions
List of sub chapters
9 Maths- Introduction to PolynomialsClass
9 Maths- Remainder theoremClass
9 Maths- Factorisation: Factor theoremClass
9 Maths- Factorisation: Split the middle termClass
9 Maths- Algebraic Identities: Quadratic Class
9 Maths- Algebraic Identities: Cubic Type
NCERT Solutions for Class 9 Maths Chapter 3 Coordinate Geometry
Thoroughly understand the concept of the Cartesian plane with TopperLearning’s class 9th maths ncert solutions Chapter 3 Coordinate Geometry. Learn to plot points in a Cartesian plane with our Maths textbook solutions. Our experts include crucial concept insights in these model answers to give you more information for conceptual clarity.
Two perpendicular number lines intersecting at point zero are called coordinate axes. The horizontal number line is the x-axis (denoted by X’OX) and the vertical one is the y-axis (denoted by Y’OY). The point of intersection of x-axis and y-axis is called origin and denoted by ‘O’.
Cartesian plane is a plane obtained by putting the coordinate axes perpendicular to each other in the plane. It is also called coordinate plane or xy plane. The x-coordinate of a point is its perpendicular distance from y-axis.The y-coordinate of a point is its perpendicular distance from x-axis.
The point where the x axis and the y axis intersect is represented by coordinate points (0, 0) and is called the origin. The abscissa of a point is the x-coordinate of the point. The ordinate of a point is the y-coordinate of the point. If the abscissa of a point is x and the ordinate of the point is y, then (x, y) are called the coordinates of the point. The axes divide the Cartesian plane into four parts called the quadrants (one fourth part), numbered I, II, III and IV anticlockwise from OX.
Sign of coordinates depicts the quadrant in which it lies. The coordinates of a point are of the form (+, +) in the first quadrant, (-, +) in the second quadrant, (-,-) in the third quadrant and (+,-) in the fourth quadrant.
The coordinates of a point on the x-axis are of the form (x, 0) and that of the point on y-axis are (0, y).
At our e-learning portal, you can find easy-to-use Class 9 Maths videos, revision notes, and assessment tools that can be accessed at any time. By embarking on a journey to learn Maths on your own using our support resources, you can improve your self-confidence too. However, if you face any problems while understanding chapter concepts, you can seek help from Maths experts at our ‘Ask a Doubt’ section.
Chapter 3 Coordinate Geometry Exercise Ex 3.1
Coordinate Geometry’s note from Class 9 Maths notes marks the foundation of a very easy and scoring chapter in CBSE Class 9 Maths textbook solution that has numerous references in higher grades. The questions from this exercise are an introduction to two-dimensional geometry. The solutions provided are apt and absolutely easy to comprehend with TopperLearning’s CBSE Class 9 Maths solution. Students can tally their solutions and use our doubt solver "Ask a Doubt" feature in case of doubts.
Chapter 3 Coordinate Geometry Exercise Ex 3.2
Learn about the cartesian system and the basic ideas of plotting and location point on the graph with TopperLearning’s Class 9 Maths solution. This chapter is popular in the multiple-choice question category. Refer to the most important MCQs and related questions asked from TopperLearning’s CBSE Class 9 Maths notes. Our Math experts can assist you with your doubts on our doubt solver "Ask a Doubt".
Chapter 3 Coordinate Geometry Exercise Ex 3.3
Revise using NCERT solutions for Class 9 Maths to gain complete confidence in the final exercise of this chapter with TopperLearning’s CBSE Class 9 Maths solution. Our solutions for the preparation of CBSE online class 9 include conceptual insight to ensure locating the position of an object or a point in a particular plane. Our doubt solver "Ask a Doubt" feature provides help in case of doubts.
NCERT Coordinate Geometry Class 9 Videos
NCERT Coordinate Geometry Class 9 Revision Notes
NCERT Coordinate Geometry Class 9 Most Important Questions
NCERT Coordinate Geometry Class 9 MCQ
NCERT Coordinate Geometry Class 9 FIB
NCERT Coordinate Geometry Class 9 Short Answer Questions
List of sub chapters
NCERT solutions for Class 9 Maths/Cartesian Plane
NCERT Solutions for Class 9 Maths Chapter 4 Linear Equations in Two Variables
Complete your Maths practice with the help of NCERT Solutions for Class 9 Maths Chapter 4 Linear Equations in Two Variables. TopperLearning’s Maths experts show you the steps to solve real-world problems based on linear equations in two variables. In this chapter, you can revise important concepts to enhance your ability to represent linear equations graphically and algebraically.
Linear equations may be tricky, but you can easily learn about them by watching our CBSE Class 9 Maths video lessons. Also, learn to easily plot graphs of linear equations in two variables with our textbook solutions and other resources for this Maths chapter.
Every point on the line satisfies the equation of the line and every solution of the equation is a point on the line.
A linear equation in two variables is represented geometrically by a straight line whose points make up the collection of solutions of the equation. This is called the graph of the linear equation.
x = 0 is the equation of the y-axis and y = 0 is the equation of the x-axis.
The graph of x = k is a straight line parallel to the y-axis.
For example, the graph of the equation x = 5 is as follows:
Chapter 4 - Linear Equations in Two Variables Exercise Ex. 4.1
Get acquainted with questions that involve two variables with TopperLearning’s CBSE Class 9 Maths solution. This exercise is quite simple, and our solutions make it simpler to understand them as you prepare for CBSE online class 9. Give a boost to your studies with CBSE Class 9 Maths textbook solution and also refer to our video sessions for precision. Our doubt solver "Ask a Doubt" is what you need when you have queries.
Chapter 4 - Linear Equations in Two Variables Exercise Ex. 4.2
Learn about the kinds of solutions a linear equation with two variables has with TopperLearning’s CBSE Class 9 Maths solution. This concept has reference in higher grade Maths. The conceptual insight with each solution and stepwise answer gives a holistic approach as you prepare for CBSE online class 9. Our doubt solver "Ask a Doubt" feature can help in resolving queries.
Chapter 4 - Linear Equations in Two Variables Exercise Ex. 4.3
Get extensive knowledge about plotting equations on a graph with TopperLearning’s CBSE Class 9 Maths solution. TopperLearning video solutions for such problems is highly recommended. Questions from this exercise are often asked for 3-4 marks in the final exam. Make use of our doubt solver "Ask a Doubt" feature and ask your doubts.
Chapter 4 - Linear Equations in Two Variables Exercise Ex. 4.4
The final exercise gives an idea about the solutions of linear equations. Considering the criticality of this chapter, taking our weekly tests and revising using the revision notes and TopperLearning’s CBSE Class 9 Maths solution can be an efficient way to practise. Revise using TopperLearning’s class 9th maths ncert solutions as you prepare for CBSE online class 9. Students can tally their solutions and use our doubt solver "Ask a Doubt" feature in case of doubts.
NCERT Linear equations in two variables Class 9 Videos
NCERT Linear equations in two variables Class 9 Revision Notes
NCERT Linear equations in two variables Class 9 Most Important Questions
NCERT Linear equations in two variables Class 9 MCQ
NCERT Linear equations in two variables Class 9 FIB
NCERT Linear equations in two variables Class 9 Short Answer Questions
List of sub chapters
Class 9 Maths- Formation of Linear Equations
Class 9 Maths- Solutions to Linear Equations
Class 9 Maths- Graphical representations
NCERT Solutions for Class 9 Maths Chapter 5 Introduction to Euclid’s Geometry
How to prove that two distinct lines can’t have more than one point in common? Find out by using our class 9th maths ncert solutions Chapter 5 Introduction to Euclid’s Geometry. Learn about Euclid’s five postulates. Revisit the relation between theorem and axiom by practising with TopperLearning’s chapter-specific solutions.
A point is that which has no part. A line is a breadthless length. The ends of a line are points.
A straight line is a line which lies evenly with the points on itself. A surface is that which has length and breadth only. The edges of a surface are lines. A plane surface is a surface which lies evenly with the straight lines on itself. Though Euclid defined a point, a line and a plane, but the definitions are not accepted by mathematicians. Therefore, these terms are taken as undefined.
An axiom is a statement accepted as true without proof, throughout Maths. A postulate is a statement accepted as true without proof, specifically in geometry.
Theorems are statements which are proved using definitions, axioms, previously proved statement and deductive reasoning.
Euclid’s 5 Postulates:
1. A straight line may be drawn from any one point to any other point.
2. A terminated line can be produced indefinitely.
1. A circle can be drawn with any centre and any radius.
2. All right angles are equal to one another.
3. If a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two straight lines, if produced indefinitely, meet on that side on which the sum of angles is less than two right angles.This is known as the parallel postulate.
Textbook solutions for CBSE Class 9 Maths will be useful when you sit to revise your lessons for class tests or exams. Other than NCERT Maths solutions, our video lessons, chapter notes and online practice tests will help you to understand theorems and postulates.
Chapter 5 - Introduction to Euclid's Geometry Exercise Ex. 5.1
Learn every minute detail about Euclid’s axioms, rules and postulates about geometry and answer the questions with complete precision as you prepare for CBSE online class 9. Our CBSE Class 9 Maths textbook solution helps you understand how to write solutions for each and every question. Our experts can quickly resolve your difficulties or you can use our doubt solver "Ask a Doubt" feature.
Chapter 5 - Introduction to Euclid's Geometry Exercise Ex. 5.2
Dive deep into the concept of Equivalent Versions of Euclid’s Fifth Postulate. Every solution has the detailed method as preferred by the CBSE board. Don’t miss to check out the most important questions and Multiple choice questions from this chapter. It will provide an insight into the question pattern. Direct yourself to our doubt solver "Ask a Doubt" feature in case of doubts.
NCERT Introduction to Euclids Geometry Class 9 Videos
NCERT Introduction to Euclids Geometry Class 9 Revision Notes
NCERT Introduction to Euclids Geometry Class 9 Most Important Questions
NCERT Introduction to Euclids Geometry Class 9 MCQ
NCERT Introduction to Euclids Geometry Class 9 FIB
NCERT Introduction to Euclids Geometry Class 9 Short Answer Questions
List of sub chapters
Class 9 Maths- Introduction To Euclid's Geometry
NCERT Solutions for Class 9 Maths Chapter 6 Lines and Angles
Refer to class 9th maths ncert solutions Chapter 6 Lines and Angles on TopperLearning for thorough Maths learning. Get clarity on concepts like linear pairs, vertically opposite angles, co-interior angles, alternate interior angles etc. While practicing the model solutions from this chapter, you will also learn to use the angle sum property of a triangle while solving problems.
Transversal
A line which intersects two or more lines at distinct points is called a transversal.
Pair of angles when a transversal intersects two lines.
Corresponding angles:
∠1 and ∠5
∠2 and ∠6
∠4 and ∠8
∠3 and ∠7
Alternate interior angles:
∠4 and ∠6
∠3 and ∠5
Alternate exterior angles:
∠1 and ∠7
∠2 and ∠8
Interior angles on the same side of the transversal are referred as co-interior angles/ allied angles/ consecutive interior angles and they are:
∠4 and ∠5
∠3 and ∠6
Understand the properties of angles and lines by studying the steps used by experts in the NCERT textbook solutions. The skills gained through our CBSE Class 9 Maths chapter resources can benefit you while preparing for your Class 10, Class 11 and Class 12 exams too.
Chapter 6 - Lines And Angles Exercise Ex. 6.1
Learn more about different types of angles and lines along with some axioms and postulates. These basics of Geometry are helpful even in the higher grades. Stepwise solutions with proper reasoning is the key to acing Geometry. Students are often puzzled about the solutions and hence we provide video lessons that clear all your grey areas. It is advisable to attempt the weekly tests and practise questions for clarity. Check your answers and ask your doubts using our doubt solver "Ask a Doubt" feature.
Chapter 6 - Lines And Angles Exercise Ex. 6.2
Apply your understanding of different types of angles and find the answers to the questions asked. TopperLearning’s NCERT solutions for Class 9 Maths for the chapter Lines and Angles exercise 6.2 give you the method accepted in the CBSE board for writing the solutions. Our doubt solver "Ask a Doubt" feature ensures quick resolution for all your queries.
Chapter 6 - Lines and Angles Exercise Ex. 6.3
Familiarize yourself with the Angle sum property of a triangle. Understand the theorem and its application through our video solutions. The solutions have all the necessary calculations and reasoning. Refer to CBSE Class 9 Maths Chapter 6 exercise 6.3 solution. Get all your concerns sorted with our doubt solver "Ask a Doubt" feature.
NCERT Lines and angles Class 9 Videos
NCERT Lines and angles Class 9 Revision Notes
NCERT Lines and angles Class 9 Most Important Questions
NCERT Lines and angles Class 9 MCQ
NCERT Lines and angles Class 9 FIB
NCERT Lines and angles Class 9 Short Answer Questions
List of sub chapters
Class 9 Maths- Basic concepts of Geometry
Class 9 Maths- Parallel-lines-and-Transversals
Class 9 Maths- Parallel lines and Co-interior angles
Class 9 Maths- Angle sum property of a Triangle
NCERT Solutions for Class 9 Maths Chapter 7 Triangles
Do you struggle to prove that the two triangles given in a textbook question are congruent? Do you find it difficult to explain the concept of SSS congruence in a Maths problem? If yes, then our class 9 solutions for Chapter 7 Triangles will be of immense help. These are model answers that Maths experts have developed to help students get conceptual clarity.
What are congruent figures?
Two figures are said to be congruent, if they are of the same shape and of the same size.
Two circles of the same radii are congruent.
Two squares of the same sides are congruent.
Congruent triangles
If two triangles ABC and DEF are congruent under the correspondence A ↔ D, B ↔ E and C ↔ F, then symbolically, it is expressed as Δ ABC ≅ Δ DEF.
In congruent triangles, corresponding parts are equal. We write in short ‘CPCT’ for corresponding parts of congruent triangles.
TopperLearning’s NCERT textbook solutions are easily available online for students trying to practise and understand the properties of triangles. You can use these chapter solutions along with our practice tests, concept videos, and CBSE Class 9 CBSE sample paper to effectively revise your Maths lessons.
Chapter 7 - Triangles Exercise Ex. 7.1
What are the criteria for proving that two triangles are congruent? How can you apply the test of congruencies to the given triangles? The answers to these questions are provided with apt methodology as accepted by the CBSE board by our subject experts. Refer to NCERT solutions for Class 9 Maths for Chapter 7 and exercise 7.1. Students can tally their solutions and use our doubt solver "Ask a Doubt" feature in case of doubts.
Chapter 7 - Triangles Exercise Ex. 7.2
Let us understand triangles better with some special properties about different types of triangles proved with basic theorems well explained in our video sessions. Refer to these maths solutions after understanding the theorems and clear all your doubts with our special feature “Ask a Doubt” where all your doubts will be catered round the clock.
Chapter 7 - Triangles Exercise Ex. 7.3
The congruency of triangles can be proved through various tests. These tests also are important for higher grade Maths hence a strong foundation is mandatory. On referring to NCERT solutions for Class 9 Maths, do take the weekly test for thorough precision. Our doubt solver "Ask a Doubt" feature takes care of all your doubts.
Chapter 7 - Triangles Exercise Ex. 7.4
The next step is about discussing the inequalities in a triangle and also about proving them. Each theorem has its applications in the questions of the exercise, hence refer to the CBSE Class 9 Maths Chapter 7 exercise 7.4 solution for free textbook solutions. Our doubt solver "Ask a Doubt" feature can help in resolving difficulties instantly.
Chapter 7 - Triangles Exercise Ex. 7.5
Get to know the in-depth concept about triangles with class 9 maths solutions. Do take the weekly test for thorough precision. Although this exercise is optional, it is always wise to have a look at the questions and tally your solutions. Seek help using our doubt solver "Ask a Doubt" feature and math experts will answer all your difficulties.
NCERT Triangles Class 9 Videos
NCERT Triangles Class 9 Revision Notes
NCERT Triangles Class 9 Most Important Questions
NCERT Triangles Class 9 Short Answer Questions
List of sub chapters
Class 9 Maths- Congruence criteria: SAS and ASA
Class 9 Maths- Congruence criteria: SSS and RHS
Class 9 Maths- Properties of Isosceles Triangle
Class 9 Maths- Inequalities in a Triangle
NCERT Solutions for Class 9 Maths chapter 8 Quadrilaterals
Learn to provide Mathematical proofs easily with TopperLearning’s class 9 solutions Chapter 8 Quadrilaterals. Can a parallelogram be a rhombus? How? Learn by practising with our solutions by Maths experts. Understand how to express your understanding of quadrilaterals such as a parallelogram and rhombus, and provide clear explanations in your answers.
What is a quadrilateral?
A quadrilateral is a closed figure obtained by joining four points (with no three points collinear) in an order.Here, ABCD is a quadrilateral.Angle sum property of a quadrilateralSum of all the angles of a quadrilateral is 360°. This is known as the angle sum property of a quadrilateral.Do watch a problem solving video on this chapter.
Here, ABCD is a quadrilateral.Angle sum property of a quadrilateralSum of all the angles of a quadrilateral is 360°. This is known as the angle sum property of a quadrilateral.
| Name of a quadrilateral | Properties |
| Parallelogram: A quadrilateral with each pair of opposite sides parallel.
| Opposite sides are equal.Opposite angles are equal.Diagonals bisect one another. |
| Rhombus: A parallelogram with sides of equal length. | All properties of a parallelogram.Diagonals are perpendicular to each other. |
| Rectangle: A parallelogram with all angles right angle. | All the properties of a parallelogram.Each of the angles is a right angle.Diagonals are equal. |
| Square: A rectangle with sides of equal length. | All the properties of a parallelogram, a rhombus and a rectangle. |
| Kite: A quadrilateral with exactly two pairs of equal consecutive sides. | The diagonals are perpendicular to one another.One of the diagonals bisects the other.If ABCD is a kite, then ∠B = ∠D but ....∠A ≠∠C. |
| Trapezium: A quadrilateral with one pair of opposite sides parallel is called trapezium. | One pair of opposite sides parallel. |
Chapter 8 - Quadrilaterals Exercise Ex. 8.1
You can score full marks in questions based on quadrilaterals by revising key concepts with our CBSE Class 9 Maths textbook solutions. If you find any of the concepts to be mind-boggling, discuss your doubts with Maths experts through our ‘Ask a Doubt’ platform.Learn all the basic properties and types of quadrilaterals and boost your score with the help of TopperLearning’s CBSE Class 9 Maths textbook solution. Our experts can quickly resolve your difficulties when you post them on our doubt solver "Ask a Doubt" feature.
Chapter 8 - Quadrilaterals Exercise Ex. 8.2.
Understand the midpoint theorem with the help of our video solutions for free textbook solutions and then give your best shot at the solutions of this exercise. Tally your answers with TopperLearning’s CBSE Class 9 Maths textbook solution and use our doubt solver "Ask a Doubt" feature in case of doubts.
NCERT Quadrilaterals Class 9 Videos
NCERT Quadrilaterals Class 9 Revision Notes
NCERT Quadrilaterals Class 9 Most Important Questions
NCERT Quadrilaterals Class 9 MCQ
NCERT Quadrilaterals Class 9 FIB
NCERT Quadrilaterals Class 9 Short Answer Questions
List of sub chapters
Class 9 Maths- Types and Angle sum property
Class 9 Maths- Parallelograms basic properties
Class 9 Maths- Angle relations in Parallelogram
Class 9 Maths- Parallelograms diagonal properties
Class 9 Maths- Mid-Point Theorem
NCERT Solutions for Class 9 Maths Chapter 9 Circles
Score marks in short answer questions easily by practising with our class 9 maths solutions Chapter 9 Circles. Write and practise with TopperLearning’s expert solutions for long answer questions based on chords. By revising a variety of textbook questions, you’ll learn how to prove chord properties in a step-wise format.
What is a Circle?
A circle is a collection (set) of all those points in a plane, each one of which is at a constant distance from a fixed point in the plane.
The fixed point is called the centre and the constant distance is called the radius of the circle.
Division of a plane using circle
A circle divides the plane on which it lies into three parts: inside the circle, the circle and outside the circle.
All the points lying inside a circle are called its interior points and all those points which lie outside the circle are called its exterior points.
The collection (set) of all interior points of a circle is called the interior of the circle while the collection (set) of all exterior points of a circle is called the exterior of the circle.
Arc of the circle
A (continuous) part of a circle is called an arc of the circle. The arc of a circle is denoted by the symbol ‘⌒’.
When an arc is formed, it divides the circle into two pieces (between the points A and B), the smaller one and the longer one. The smaller one is called the minor arc of the circle, and the greater one is called the major arc of the circle.
With CBSE Class 9 Maths chapter solutions, learn the application of important concepts such as RHS congruence rule, angle sum property of a triangle etc. This knowledge will help you think logically and write correct answers in your Maths exam. Other than expert solutions, you may want to use CBSE sample paper class 9, online mock tests, concept videos etc. to revise circles for exam preparation.
Chapter 9 - Circles Exercise Ex. 9.1
Familiarize yourself to various basic properties and terminologies of a circle from the CBSE Class 9 syllabus. Refer to the CBSE Class 9 Maths Chapter 10 exercise 10.1 solution from free textbook solutions. Ask all your queries on our doubt solver "Ask a Doubt" feature and get it solved by our experts.
Chapter 9 - Circles Exercise Ex. 9.2
Get the complete solution to this short exercise based on the basic theorems with a proper stepwise solution from CBSE Class 9 syllabus. These questions have previously been asked in CBSE board exams. Refer to CBSE Class 9 Maths sample paper to understand the types of questions asked in the exam. Use the doubt solver "Ask a Doubt" feature for all your difficulties.
Chapter 9 - Circles Exercise Ex. 9.3
Practise problems based on properties of the circle regarding chords through TopperLearning’s NCERT solutions for class 9 Maths. Our solutions have proper steps and reasoning as accepted by the CBSE board. TopperLearning’s doubt solver "Ask a Doubt" feature provides quick assistance to all your queries.
Chapter 9 - Circles Exercise Ex. 9.4
Discover questions on Equal Chords and Their Distances from the Centre and refer to TopperLearning’s class 9 maths solutions detailed stepwise approach-based solutions. It is advisable to refer to the most important questions from this chapter from TopperLearning’s study material. Students can check their solutions and use our doubt solver "Ask a Doubt" feature to ask related queries.
Chapter 9 - Circles Exercise Ex. 9.5
Get introduced to cyclic quadrilaterals and understand all the basic features of it with TopperLearning’s NCERT solutions for class 9 Maths. This is the easiest and also the most scoring part of this chapter. Our subject experts have solved these questions with utmost clarity and detailed approach as accepted by the CBSE board. Check your answers and use our doubt solver "Ask a Doubt" feature for any concerns.
NCERT Circles Class 9 Revision Notes
NCERT Circles Class 9 Most Important Questions
NCERT Circles Class 9 Short Answer Questions
List of sub chapters
Class 9 Maths- Introduction to Circles
Class 9 Maths- Angle subtended by the chord
Class 9 Maths- Perpendicular from centre to chord
Class 9 Maths- Properties of equal chords
Class 9 Maths- Cyclic Quadrilaterals
NCERT Solutions for Class 9 Maths Chapter 10 Heron’s Formula
Get answers on Heron’s formula and the applications of Heron’s formula in this chapter. At TopperLearning, find free CBSE Class 9 Maths solutions to the 2 exercises in Chapter 10 from the Maths NCERT textbook. Using Heron’s formula, learn to find the area of triangles and the area of polygons.
The region enclosed within a simple closed figure is called its area. Area of a triangle = 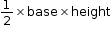
Area of an equilateral triangle = 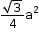 sq units, where ‘a’ is the side length of an equilateral triangle.
sq units, where ‘a’ is the side length of an equilateral triangle.
Semi-perimeter is half of the perimeter. If a, b and c denote the lengths of the sides of a triangle, then the area of the triangle is calculated by using Heron's formula, as given below:
Area of triangle = 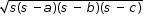 ,s = semi - perimeter =
,s = semi - perimeter = 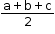 . For every triangle, the values of (s – a), (s – b), and (s – c) are positive. Area of a quadrilateral can be calculated by dividing the quadrilateral into two triangles and using Heron's formula for calculating area of each triangle.
. For every triangle, the values of (s – a), (s – b), and (s – c) are positive. Area of a quadrilateral can be calculated by dividing the quadrilateral into two triangles and using Heron's formula for calculating area of each triangle.
Chapter 10 - Heron's Formula Exercise Ex. 10.1
Discover the methodology of calculating the area of a triangle Heron’s formula with TopperLearning’s class 9 maths solutions. Make use of our doubt solver "Ask a Doubt" feature for quick assistance on problems by our Math experts.
Chapter 10 - Heron's Formula Exercise Ex. 10.2
Get extensive knowledge about finding the area of a quadrilateral using Heron’s formula with this exercise. TopperLearning video solution for such problems is highly recommended. Questions from this exercise are often asked for 3-4 makes in final exams. Skilled experts address your doubts instantly when you use our doubt solver "Ask a Doubt" feature in case of doubts.
NCERT Heron’s Formula Class 9 Videos
NCERT Heron’s Formula Class 9 Revision Notes
NCERT Heron’s Formula Class 9 Most Important Questions
NCERT Heron’s Formula Class 9 MCQ
NCERT Heron’s Formula Class 9 FIB
NCERT Heron’s Formula Class 9 Short Answer Questions
List of sub chapters
Class 9 Maths- Introduction to Herons formula
Class 9 Maths- Application of Herons formula
NCERT Solutions for Class 9 Maths Chapter 11 Surface Areas and Volumes
Revise the most important concepts in the chapter with class 9 maths solutions Chapter 11 Surface Areas and Volumes. In this chapter, TopperLearning gives you access to some of the best textbook solutions to understand the surface area of objects and spaces using the given data. Practise calculating the lateral surface area of a cubical box or the CSA of a given cylindrical pipe with our solutions.
If l, b, h denote respectively the length, breadth and height of a cuboid, then:
Lateral surface area or Area of four walls = 2(ℓ + b) h
Total surface area = 2(ℓb + bh + hℓ)
Volume = ℓ × b × h
Diagonal of a cuboid = 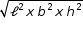
If the length of each edge of a cube is 'a' units, then:
Lateral surface area = 4 x (edge)2
Total surface area = 6 x (edge)²
Volume = (edge)3
Diagonal of a cube = √3 x edge
If r and h respectively denote the radius of the base and the height of a right circular cylinder, then:
Area of each end or Base area = 𝜋r²
Area of curved surface or lateral surface area = perimeter of the base x height = 2𝜋rh
Total surface area (including both ends) = 2𝜋rh + 2𝜋r² = 2𝜋r (h + r)
Volume = Area of the base x height = 𝜋r²h
On our e-learning portal, we provide free access to NCERT textbook solutions and other CBSE Class 9 Maths study materials. To practise Maths, you may refer to our online practice tests, video lessons, practice question papers and more.
Chapter 11 - Surface Areas and Volumes Exercise Ex. 11.1
Get acquainted with questions about finding the surface area and volume of a cube and cuboid. This exercise is quite simple, and our solutions make it simpler to understand them. Get a boost in your studies with CBSE Class 9 Maths textbook solution and also refer to our video sessions for a better grip on the concepts. TopperLearning’s doubt solver "Ask a Doubt" feature gives quick assistance to all your queries.
Chapter 11 - Surface Areas and Volumes Exercise Ex. 11.2
Solve problems about finding surface area of a Right Circular Cylinder with TopperLearning’s NCERT solutions for class 9 Maths. Direct yourself to our doubt solver "Ask a Doubt" feature in case of doubts.
Chapter 11 - Surface Areas and Volumes Exercise Ex. 11.3
Learn how to solve questions on finding curved surface and total surface area of a right circular cone with TopperLearning’s NCERT solutions for Class 9 Maths. Check your solutions and use our doubt solver "Ask a Doubt" feature in case of doubts.
Chapter 11 - Surface Areas and Volumes Exercise Ex. 11.4
Practise problems on finding curved surface and total surface area of a sphere and a hemisphere with CBSE Class 9 Maths textbook solution. Use our doubt solver "Ask a Doubt" feature and get your doubts resolved.
Chapter 11 - Surface Areas and Volumes Exercise Ex. 11.5
Through TopperLearning’s NCERT solutions for class 9 Maths for CBSE Class 9 Maths Chapter 13 exercise 13.9 solution, ace solving questions about the volume of a cuboid.
Chapter 11 - Surface Areas and Volumes Exercise Ex. 11.6
Master solving problems about finding the volume of a cylinder with TopperLearning solutions for Class 9th Maths. Our experts will help you with your doubts with our doubt solver "Ask a Doubt."
Chapter 11 - Surface Areas and Volumes Exercise Ex. 11.7
Gain expertise by solving every question on finding the volume of a right circular cone with TopperLearning’s CBSE Class 9 Maths textbook solution. Get your doubts quickly resolved using our doubt solver "Ask a Doubt."
Chapter 11 - Surface Areas and Volumes Exercise Ex. 11.8
Compute the volume of a sphere and hemisphere with TopperLearning’s NCERT solutions for class 9 Maths. Our doubt solver "Ask a Doubt" provides quick clarification on your doubts.
Chapter 11 - Surface Areas and Volumes Exercise Ex. 11.9
Understand the in-depth concepts of surface areas and volumes in this chapter with NCERT solutions for Class 9 Maths when you take the weekly test. Although this exercise is optional, it is always wise to have a look at the questions and tally your solutions to gauge your preparation.
Revise using class 9 maths solutions to gain complete confidence in the final exercise of this chapter. Our solutions with conceptual insights will help you locate the position of an object or a point in a particular plane. If there are any difficulties, use our doubt solver "Ask a Doubt".
NCERT Surface areas and volumes Class 9 Videos
NCERT Surface areas and volumes Class 9 Revision Notes
NCERT Surface areas and volumes Class 9 Most Important Questions
NCERT Surface areas and volumes Class 9 MCQ
NCERT Surface areas and volumes Class 9 FIB
NCERT Surface areas and volumes Class 9 Short Answer Questions
List of sub chapters
Class 9 Maths- Surface area of a Cube and Cuboid
Class 9 Maths- Surface Area Of A Cylinder
Class 9 Maths- Surface Area Of A Cone
Class 9 Maths- Sphere And Hemisphere
Class 9 Maths- Volume Of A Cuboid
Class 9 Maths- Volume Of A Cylinder
Class 9 Maths- Volume Of A Cone
Class 9 Maths- Sphere And Hemisphere
NCERT Solutions for Class 9 Maths Chapter 12 Statistics
How is data collected? What are the ways to present data? Discover the answers for these important questions in our class 9 maths solutions Chapter 12 Statistics. Practise the presentation of data in the form of histograms and bar graphs with our model answers for questions in the NCERT book.
A measure of central tendency tries to estimate the central value which represents the entire data.
The three measures of central tendency for ungrouped data are mean, mode and median.
The mean value of a variable is defined as the sum of all the values of the variable divided by the number of values.
If x1, x2, x3 .... , xn are n values of a variable X, then the arithmetic mean of these values is given by:
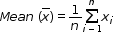
If a variate X takes values x1, x2, x3.... , xn with corresponding frequencies f1, f2, f3,... fn respectively, then arithmetic mean of these values is given by
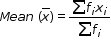
Median is the value of middle most observation(s).
The median is calculated only after arranging the data in ascending order or descending order.
Median = 
Mode of a statistical data is the value of that variate which has the maximum frequency.
The variate corresponding to the highest frequency is to be taken as the mode and not the frequency.
The disadvantage of arithmetic mean is that it is affected by extreme values.
The disadvantage of mode is that it is not uniquely defined in many cases.
At TopperLearning, you can access our online NCERT textbook solutions for Class 9 Maths to revise mean, mode and median calculations. The chapter solutions also show the accurate way to construct a frequency distribution table according to the given information. You can learn statistics on our learning portal through video lessons, online practice tests and other Maths resources as well.
Chapter 12 - Statistics Exercise Ex. 12.1
Learn everything about primary, secondary, grouped and ungrouped data with CBSE Class 9 Maths textbook solution. This chapter lays the foundation for an important concept in Maths. Our Math experts can assist you with your doubts on our doubt solver "Ask a Doubt".
Chapter 12 - Statistics Exercise Ex. 12.2
Get extensive knowledge about the classification of grouped and ungrouped data in a frequency with TopperLearning’s NCERT solutions for Class 9 Maths. TopperLearning’s video solutions for such problems is highly recommended to develop a conceptual understanding of the topic. Questions from this exercise are often asked for 3-4 marks in the final examinations. Use our doubt solver "Ask a Doubt" feature and ask your queries.
Chapter 12 - Statistics Exercise Ex. 12.3
Obtain a detailed methodology of solving questions regarding the graphical representation of data with our class 9 maths solutions. Our experts quickly resolve your difficulties whenever you use our doubt solver "Ask a Doubt" feature.
Chapter 12 - Statistics Exercise Ex. 12.4
Understand the process of finding mean, median and mode using different methods in a step-wise approach with TopperLearning’s Maths solutions. Check your answers and ask your doubts using our doubt solver "Ask a Doubt" feature.
The most effective source while preparing for CBSE online class 9 is an audio-video study material through our video sessions. TopperLearning’s study material – particularly CBSE Class 9 notes and free textbook solutions – proves to be quite effective in your preparation. Get all your concerns addressed with our doubt solver "Ask a Doubt" feature.
NCERT Statistics Class 9 Videos
NCERT Statistics Class 9 Revision Notes
NCERT Statistics Class 9 Most Important Questions
NCERT Statistics Class 9 Short Answer Questions
List of sub chaptesrs
Class 9 Maths- Grouping And Tabulation Of Data
Class 9 MathS- Graphical Representation Of Data
Class 9 Maths- Measures Of Central Tendency
CBSE Class 9 Chapter-wise Marks Weightage
TopperLearning has made available an organised method for you to know the chapter-wise marks weightage. This helps in focusing better on the chapters with higher scoring potential. Prepare each of these chapters with TopperLearning’s class 9 maths solutions and also solve CBSE Class 9 sample paper 2020-21 to gain confidence.
COURSE STRUCTURE CBSE CLASS 9
| Units | Unit Name | Marks |
| I | NUMBER SYSTEMS | 08 |
| II | ALGEBRA | 17 |
| III | COORDINATE GEOMETRY | 04 |
| IV | GEOMETRY | 28 |
| V | MENSURATION | 13 |
| VI | STATISTICS & PROBABILITY | 10 |
| Total | 80 |
CBSE Class 9 Maths – Standard Question Paper (2021-2022)
The paper pattern will help you prepare for exams by focusing on the areas that need more effort. CBSE question papers are designed in a way that assesses the understanding of a student’s grasp of a concept. Hence, we provide you with the paper design along with CBSE Class 9 sample paper 2020-21 to help you score higher marks.
|
Sr. No. |
Typology of Questions |
Total Marks | % Weightage (approx.) |
|
1 | Remembering: Exhibit memory of previously learned material by recalling facts, terms, basic concepts, and answers. Understanding: Demonstrate understanding of facts and ideas by organizing, comparing, translating, interpreting, giving descriptions, and stating main ideas |
43 |
54 |
|
2 | Applying: Solve problems to new situations by applying acquired knowledge, facts, techniques and rules in a different way. | 19 | 24 |
|
3 | Analysing : Examine and break information into parts by identifying motives or causes. Make inferences and find evidence to support generalizations Evaluating: Present and defend opinions by making judgments about information, the validity of ideas, or quality of work based on a set of criteria. Creating: Compile information together in a different way by combining elements in a new pattern or proposing alternative solutions. |
18 |
22 |
| Total | 80 | 100 |
|
| INTERNAL ASSESSMENT |
| 20 MARKS |
|
| Pen Paper Test and Multiple Assessment (5+5)Portfolio |
| 10 Marks |
|
| Portfolio | 05 Marks | |
|
| Lab Practical (Lab activities to be done from the prescribed books)10 Marks |
| 05 Marks |
Benefits of NCERT Solutions CBSE Class 9 Maths
You can avail chapter-wise detailed solutions to the questions of the NCERT books with TopperLearning’s NCERT solutions for Class 9 Maths as per the revised CBSE curriculum. The answers are provided with TopperLearning’s class 9 maths solutions have an objective of helping students compare their answers with the sample answers. This will not only help you in acing your grades, but also help build a strong foundation.
The most effective material while preparing for CBSE online class 9 and CBSE Class 9 syllabus is video sessions. This will help any student with the summary of the chapter for a quick revision. TopperLearning’s revision notes also help for your last-minute study preparation.
These notes will help you in each and every step of your preparation. You can refer to the summaries and mind maps for quick revision. There are more than 2,000 questions for your smooth practice associated with various tests for assessing your knowledge. You also have the option of asking your doubts using our ‘Ask a Doubt’ feature, which will give you a quick resolution of your queries. Our experts will help you solve your doubts within 24 hours.
CBSE Class 9 sample paper 2020-21 is a section for assessing the knowledge one has gained using all the above parameters. Solve CBSE Class 9 Maths sample paper to test your skills and compare your solutions.
Why should I get TopperLearning NCERT Solutions for CBSE Class 9?
1. 400+ Video Lectures, 200+ Revision Notes, 12,000+ Question Banks, 50+ CBSE sample paper class 9.
2. Strong Emphasis on latest NCERT 9th Standard Syllabus for 2018–19.
3. Doubt Solving by Professionals option available.
4. Chapter-wise solutions by experts.
5. Free assessment tools & guidance by previous Toppers.
6. CBSE Class 9 Preparation tips.
7. In-depth understanding of all the concepts.
8. Quick revision & improvement in results.
Clear all your doubts instantly at our “Ask a Doubt” section, post them and we will resolve them at the earliest. Get expert help and guidance at your comfort. To ask your doubts, click here.
CBSE Class 9 Maths Frequently Asked Questions
You may find Math difficult only if you are unclear with the concepts. If you keep your basics clear, understand the reason behind each step and practise similar problems, you’ll certainly become more confident.
CBSE board designs a pattern for schools to follow for terminal and final examinations. Every detail regarding the marking scheme and the paper pattern along with the samples papers is available for reference and practice to make it easier for you.
Using our Ask a Doubt feature, you can ask your doubts at any hour and our experts will help you with it.
Theorems are a significant part of Mathematics. They are often asked in CBSE board exams, so it is necessary to have a grip on them. It best to refer to concept videos in order to have a satisfactory explanation.
Our study material is well equipped with all the textbook solutions. Every chapter has been solved in an apt manner, making it simpler for students to understand. Find just what you need for your preparation at CBSE Class 9 Maths. You may also refer to the CBSE Class 9 Maths samples papers to understand the types of questions asked in the exam.
Yes. TopperLearning’s study material is well equipped for all kinds of solutions including deleted syllabus of CBSE Class 9. We are completely updated as per the revised CBSE guidelines and can help you with the deleted syllabus of CBSE Class 9.
TopperLearning caters to every need of a student and so the solutions for CBSE Class 9 Science are also available. We also have solutions for CBSE Class 9 English to ensure students are completely prepared for their exams.
TopperLearning’s study material comprises everything for the CBSE Class 9 syllabus including video sessions, NCERT textbook solutions, revision notes, weekly tests, CBSE Class 9 sample paper 2020-21 and more. You may also refer to CBSE Class 9 notes and find everything that you need.
Yes. We have the entire CBSE study material as per revised and updated CBSE Guidelines. Refer to CBSE Class 9 syllabus and you will find everything that you need.
Yes. We have most important questions for last-minute revision. You may also refer to CBSE Class 9 Maths samples papers and CBSE Class 9 sample paper 2020-21 to understand the types of questions asked in the exam.
Class 9th Maths NCERT Solutions comprises 15 chapters, each explained in detail by the experts within the pdf. Both questions and solutions are provided for students to understand the topic better. However, certain chapters hold a higher weightage than others. The names of those chapters are mentioned below:
- Rationalisation
- Non Terminating Numbers
- Algebraic Identities
- Laws Of Exponents
- Coordinate Geometry
- Remainder Theorem
- Herons Formula
- Zeros Of Polynomials
- Euclid's Geometry
- Pair Of Linear Equations In Two Variables
- Angle Sum Property Of A Triangle
The majority of the questions appear from these topics, and therefore, students must prepare them thoroughly to secure good marks in the examination. In addition, the Class 9 Maths Solutions are written in lucid language to assist students in learning and comprehending the idea. Therefore, the Class 9 Maths Solutions aim to help candidates achieve better marks than other candidates sitting for the Class 10 board examination and prepare brilliantly.
The chapter-wise answers of the Class 9th Maths NCERT Solutions are available on the official website of NCERT. It is available in pdf form. You can download the pdf for reference. Apart from this, it is also accessible on our official website.
The answers to questions in Class 9 Maths Solutions are the best study guides available for students. These CBSE NCERT Solutions for Class 9 Maths 2021-22 help students better understand the topics covered in the textbook. Solving textbook problems allows students to gauge their preparation and subject understanding. In addition, the answers in the books might help students solve the questions rapidly.
The NCERT Solutions for Class 9 Maths list includes chapter-by-chapter answers to questions from the NCERT Book for Class 9 Maths, explicitly written and rationally while conforming to the textbook's goals. The NCERT Solutions for Class 10 can be used as additional resources and study materials by candidates. Additionally, as part of their test preparation, students will benefit immensely from practising NCERT textbook practise solutions.
You can easily download the Class 9th Maths NCERT Solutions from TopperLearning by following the steps mentioned below:
- Visit our official website https://www.topperlearning.com/
- Now click on "Study Materials" and select "Textbook Solutions".
- A page will appear. Here, click on the "NCERT Solutions for Class 9". The website will direct you to a page where you will find NCERT Solutions for different subjects.
- Click on "Mathematics". Another page will display.
- Here, you will find descriptions of each chapter in the Class 9 Maths syllabus.
- Click on the chapter whose NCERT Solutions you are looking for.
- A page will appear to download the Class 9 Maths Solutions and study them to effectively prepare for the board exams.
You can download pdfs for all the chapters and practise the questions mentioned to grasp each concept better. NCERT Solutions for Class 9 Maths are formulated in an easy-to-understand language, and thus, you won't face much difficulty comprehending the sums.

