Class 9 NCERT Solutions Maths Chapter 10 - Heron's Formula
Ex. 10.1
Heron's Formula Exercise Ex. 10.1
Solution 1
Side of traffic signal board = a
Perimeter of traffic signal board = 3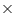 a
a
Perimeter of traffic signal board = 3
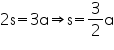
By Heron's formula
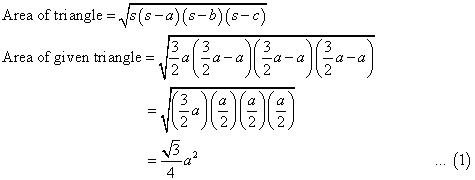
Perimeter of traffic signal board = 180 cm
Side of traffic signal board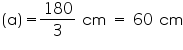
Side of traffic signal board
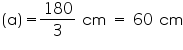
Using equation (1), area of traffic of signal board 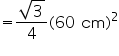
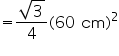
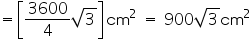
Solution 2
We may observe that sides of triangle a, b, c are of 122 m, 22 m, and 120 m respectively
Perimeter of triangle = (122 + 22 + 120) m
2s = 264 m
s = 132 m
By Heron's formula
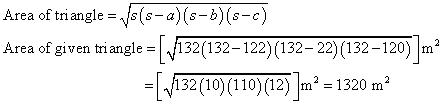
Perimeter of triangle = (122 + 22 + 120) m
2s = 264 m
s = 132 m
By Heron's formula
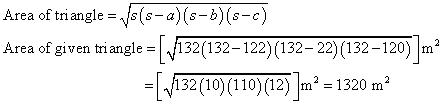
Rent of 1 m2 area per year = Rs.5000
Rent of 1 m2 area per month = Rs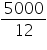
Rent of 1 m2 area per month = Rs
Rent of 1320 m2 area for 3 months 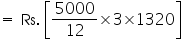
= Rs.(5000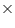 330) = Rs.1650000
330) = Rs.1650000
So, company had to pay Rs.1650000.
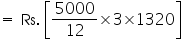
= Rs.(5000
So, company had to pay Rs.1650000.
Solution 3
We may observe that the area to be painted in colour is a triangle, having its sides as 11 m, 6 m, and 15 m.
Perimeter of such triangle = (11 + 6 + 15) m
2 s = 32 m
s = 16 m
By Heron's formula
Perimeter of such triangle = (11 + 6 + 15) m
2 s = 32 m
s = 16 m
By Heron's formula
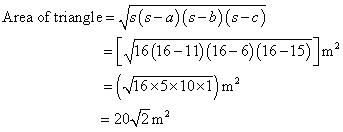
So, the area painted in colour is 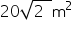 .
.
Solution 4
Let third side of triangle be x.
Perimeter of given triangle = 42 cm
18 cm + 10 cm + x = 42
x = 14 cm
Perimeter of given triangle = 42 cm
18 cm + 10 cm + x = 42
x = 14 cm

By Heron's formula
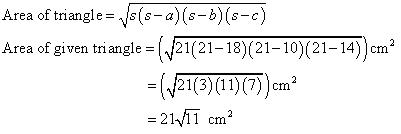
Solution 5
Let the common ratio between the sides of given triangle be x.
So, side of triangle will be 12x, 17x, and 25x.
Perimeter of this triangle = 540 cm
12x + 17x + 25x = 540 cm
54x = 540 cm
x = 10 cm
Sides of triangle will be 120 cm, 170 cm, and 250 cm.
So, side of triangle will be 12x, 17x, and 25x.
Perimeter of this triangle = 540 cm
12x + 17x + 25x = 540 cm
54x = 540 cm
x = 10 cm
Sides of triangle will be 120 cm, 170 cm, and 250 cm.
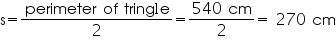
By Heron's formula
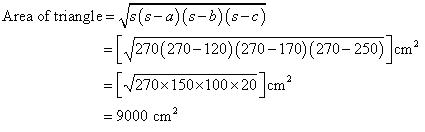
So, area of this triangle will be 9000 cm2.
Solution 6
Let third side of this triangle be x.
Perimeter of triangle = 30 cm
12 cm + 12 cm + x = 30 cm
x = 6 cm
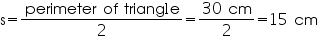
Perimeter of triangle = 30 cm
12 cm + 12 cm + x = 30 cm
x = 6 cm
By Heron's formula


