Class 9 NCERT Solutions Maths Chapter 5 - Introduction to Euclid's Geometry
Ex. 5.1
Introduction to Euclid's Geometry Exercise Ex. 5.1
Solution 1
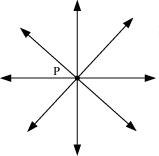
(i) False as through a single point infinite number of lines can pass. Here in the figure we may find that there are infinite numbers of lines, which are passing through a single point P.
(ii) False as through two district points only one line can pass. Here in the following figure we may find that there is only one single line that can pass through two distinct points P and Q.

(iii) True a terminated line can be produced indefinitely on both the sides.
Let AB be a terminated line. We may find that it can be produced indefinitely on both the sides.

(iv) True if two circles are equal, their centre and circumference will coincide and hence radii will be equal.
(v) True. It is given that AB and XY are two terminated lines and both are equal to a third line PQ. Euclid's first axiom states that things which are equal to the same thing are equal to one another. So, the lines AB and XY will be equal to each other.

(ii) False as through two district points only one line can pass. Here in the following figure we may find that there is only one single line that can pass through two distinct points P and Q.
(iii) True a terminated line can be produced indefinitely on both the sides.
Let AB be a terminated line. We may find that it can be produced indefinitely on both the sides.

(iv) True if two circles are equal, their centre and circumference will coincide and hence radii will be equal.
(v) True. It is given that AB and XY are two terminated lines and both are equal to a third line PQ. Euclid's first axiom states that things which are equal to the same thing are equal to one another. So, the lines AB and XY will be equal to each other.
Solution 2
(i) Parallel Lines:
If the perpendicular distance between two lines is always constant, these are called parallel lines. In other words we may say that the lines which never intersect each other are called parallel lines.
To define parallel line, we must know about point, lines and distance between lines and point of intersection.
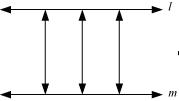
To define parallel line, we must know about point, lines and distance between lines and point of intersection.

(ii) Perpendicular lines:
If two lines intersect each other at 90 , these are called perpendicular lines. We need to define line and the angle before defining perpendicular lines.
If two lines intersect each other at 90 , these are called perpendicular lines. We need to define line and the angle before defining perpendicular lines.
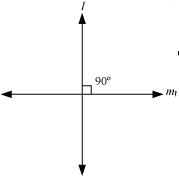
(iii) Line segment:
A straight line drawn from any point to any other point is called as line segment. To define line segment, we must know about point and line segment.
A straight line drawn from any point to any other point is called as line segment. To define line segment, we must know about point and line segment.
(iv) Radius of a circle:
It is the distance between the centre of a circle to any point lying on the circle. To define radius of circle, we must know about point and circle.
It is the distance between the centre of a circle to any point lying on the circle. To define radius of circle, we must know about point and circle.
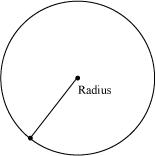
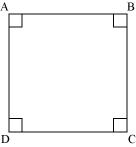
(v) Square:
A square is a quadrilateral having all sides of equal length and all angles of same measure i.e. 90o . To define square, we must know about quadrilateral, side, and angle.
A square is a quadrilateral having all sides of equal length and all angles of same measure i.e. 90o . To define square, we must know about quadrilateral, side, and angle.
Solution 3
(i) There are undefined terms. They are consistent. As we have no information about line segment AB and we don't know about the position of third point C whether it is lying on the line segment AB or not, now two different cases are possible -
- The third point C lies on the line segment made by joining the points A and B.
- The third point C does not lie on the line segment made by joining the points A and B.
Yes, they are consistent as these are two different situations;
(i) the third point c lies on the line segment made by joining points A and B.
(ii)The third point does not lie on the line segment made by joining points A and B.
No, these postulates do not follow Euclid's postulates actually these are axiom.
Solution 4
Given that
AC = BC
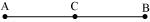
AC = BC
AC+AC=BC+AC (equals are added on both sides) ... (i)
Here, (BC + AC) coincides with AB. We know that things which coincide with one another are equal to one another.
We know that things which are equal to the same thing are equal to one another. So, from equation (i) and equation (ii), we have
AC + AC = AB
2AC = AB
Solution 5
Let us assume there are two mid-points C and D
C is mid point of AB
AC = CB
AC + AC = BC + AC (equals are added on both sides) ... (1)
Here, (BC + AC) coincides with AB. We know that things which coincide with one another are equal to one another.
 BC + AC = AB ... (2)
BC + AC = AB ... (2)
We know that things which are equal to the same thing are equal to one another. So, from equation (1) and equation (2), we have
AC + AC = AB
 2AC = AB ... (3)
2AC = AB ... (3)
Similarly by taking D as the mid-point of AB, we can prove that
2AD = AB ... (4)
From equation (3) and (4), we have
AC = CB
AC + AC = BC + AC (equals are added on both sides) ... (1)
Here, (BC + AC) coincides with AB. We know that things which coincide with one another are equal to one another.
We know that things which are equal to the same thing are equal to one another. So, from equation (1) and equation (2), we have
AC + AC = AB
Similarly by taking D as the mid-point of AB, we can prove that
2AD = AB ... (4)
From equation (3) and (4), we have
2AC = 2AD (Things which are equal to the same thing are equal to one another.)
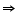 AC = AD (Things which are double of the same things are equal to one another.)
AC = AD (Things which are double of the same things are equal to one another.)
It is possible only when point C and D are representing a single point.
Hence our assumption is wrong and there can be only one mid-point of a given line segment.
It is possible only when point C and D are representing a single point.
Hence our assumption is wrong and there can be only one mid-point of a given line segment.
Solution 6
From the figure we may observe that
AC = AB + BC
BD = BC + CD
Given that AC = BD
AB + BC = BC + CD (1)
According to Euclid's axiom, we know that when equals are subtracted from equals, remainders are also equal.
Subtracting BC from the equation (1), we have
AB + BC - BC = BC + CD - BC
AB = CD
AC = AB + BC
BD = BC + CD
Given that AC = BD
AB + BC = BC + CD (1)
According to Euclid's axiom, we know that when equals are subtracted from equals, remainders are also equal.
Subtracting BC from the equation (1), we have
AB + BC - BC = BC + CD - BC
AB = CD
Solution 7
Axiom 5: The whole is greater than the part.
Let t is representing a whole quantity and only a, b, c are parts of it.
Now t = a + b + c
Clearly t will be greater than all its parts a, b and c
So, it is rightly said that the whole is greater than the part.
Let us consider another example. Let us consider a continent, let say Asia. Let us consider a country India which belongs to Asia. Now, India is a part of Asia and we can also observe that Asia is greater than India. That is why we can say that the whole is greater than the part. This is true for any thing in any part of the world, this is a universal truth.
Let t is representing a whole quantity and only a, b, c are parts of it.
Now t = a + b + c
Clearly t will be greater than all its parts a, b and c
So, it is rightly said that the whole is greater than the part.
Let us consider another example. Let us consider a continent, let say Asia. Let us consider a country India which belongs to Asia. Now, India is a part of Asia and we can also observe that Asia is greater than India. That is why we can say that the whole is greater than the part. This is true for any thing in any part of the world, this is a universal truth.

