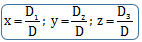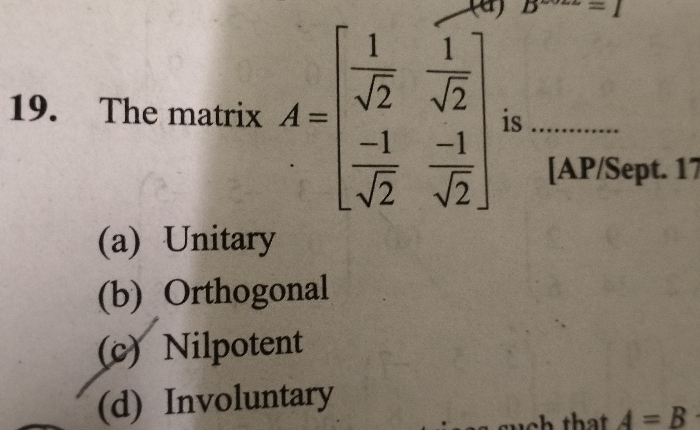Matrices and Determinants
Matrices and Determinants PDF Notes, Important Questions and Synopsis
SYNOPSIS
- Determinants
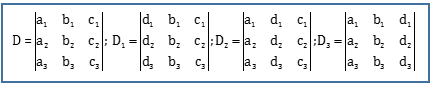
Every square matrix can be associated to a number called a Determinant.
For A → Square matrix; |A| or det A or D → denotes the determinant of A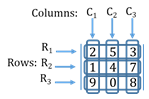
-
Sub-matrix
A matrix obtained after deleting some rows or columns is called a sub-matrix. -
Minor & Cofactor
A minor is the determinant of the sub-matrix obained by deleting the ith row and jth column.
It is denoted by Mij.
A cofactor is denoted by Cij, and it is given by Cij = (-1)i+j Mij. -
Finding Determinant
A matrix should be a square matrix of order greater than 1, A = [aij]nxn.
A determinant of a matrix A is defined as the sum of the products of elements of any one row (or column) with corresponding cofact
|A|= a11C11 + a12C12 + a13C13 (Using first row)ors.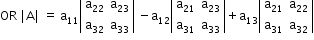
-
Properties of a Determinant
- The value of a determinant remains the same if the rows and columns are interchanged.
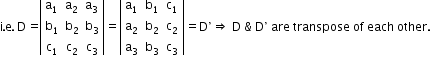
- The value of a determinant changes in sign only if any two rows (or columns) of a determinant are interchanged.
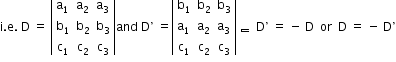
- If a determinant has any two rows (or columns) identical, then the value of the determinant is zero.
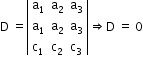
- If all the elements of any row (or column) are multiplied by the same number, then the determinant is multiplied by that number.
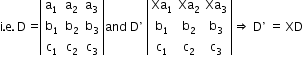
- If each element of any row (or column) can be expressed as a sum of two terms, then the determinant can be expressed as the sum of two determinants.
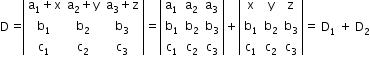
- The value of a determinant does not change by adding to the elements of any row (or columns) the same multiples of the corresponding elements of any other row.
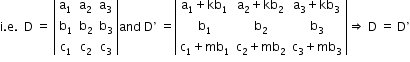
Note: While applying this property, at least one row or column must remain unchanged.
- The value of a determinant remains the same if the rows and columns are interchanged.
-
Cramer’s Rule (Determinant)
Consider three simultaneous linear equations:
a1x + b1y + c1z = d1 , a2x + b2y + c2z = d2 and a3x + b3y + c3z = d3
The solution of the above system of linear equations is :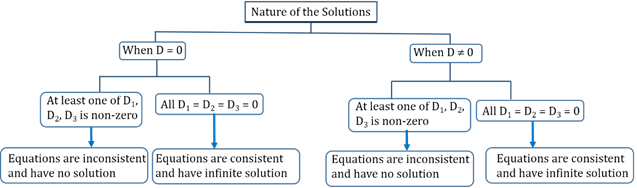
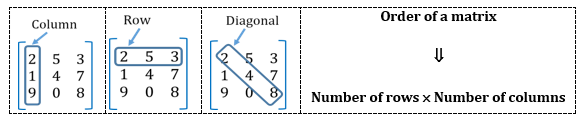
A matrix is a rectangular array/arrangement of numbers along rows and columns.
Note: A matrix A = [aij], where aij is an element of the ith row and jth column.
Row number and column number are the same for diagonal elements.
- Classification of Matrices
- Row Matrix A = [3 6 -8]
Matrix having only OR
one row. A = [1 2 6 0]
- Column Matrix
Matrix having only one column.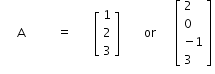
- Square Matrix
Matrix having same number of rows and columns.
- Zero (Null) Matrix
Matrix having all elements equal to zero.
Matrix having all elements equal to zero.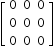
- Upper Triangular Matrix
All entries below the main diagonal are zero.
All entries below the main diagonal are zero.
- Lower Triangular Matrix
All entries above the main diagonal are zero.
- Diagonal Matrix
All entries above and below the diagonal are zero.
All entries above and below the diagonal are zero.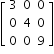
- Identity (Unit) Matrix
All diagonal entries are one and the rest are zero.
All diagonal entries are one and the rest are zero.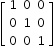
- Row Matrix A = [3 6 -8]
- Operations on Matrices
- Addition of Matrices
Order of the matrices must be same.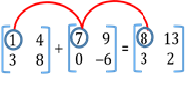
- Subtraction of Matrices
Order of the matrices must be same.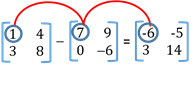
- Equality of matrices
Matrices having same order with each of their elements equal.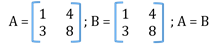
- Transpose of a Matrix
Matrix obtained after turning rows into columns and vice versa; denoted by AT.
Matrix obtained after turning rows into columns and vice versa; denoted by AT.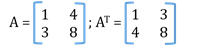
- Addition of Matrices
- Multiplication of Matrices
- Multiplication of a matrix with a scalar
Each element of the matrix is multiplied by the scalar.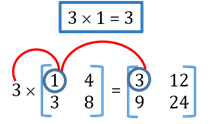
- Multiplication of two matrices
Let A and B be two matrices, then A
Let A and B be two matrices, then A ´ B is possible only if ‘No. of columns of 1st matrix = No. of rows of 2nd matrix’.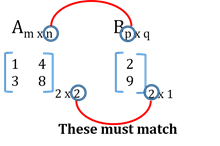
Process of Multiplication of two Matrices
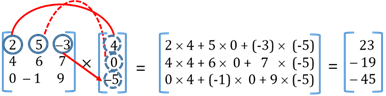
- Multiplication of a matrix with a scalar
- Inverse of a Matrix
Inverse of a matrix A is denoted by A-1 such that (matrix) (inverse of matrix) = I
i.e. A × A-1 = I or A-1 × A = I. But A × A-1 ≠ A-1 ´ A.
Steps of finding inverse of a matrix:Step I
Check whether matrix A is singular or non-singular, i.e.
|A| = 0 Þ Singular
|A| ≠ 0 Þ Non-singularStep II
If matrix A is non-singular, then find the value of determinant of A and also find the adjoint matrix A.
Step III
Use the formula
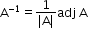
Note: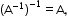 if A is non-singular.
if A is non-singular.
If A = diag (a11, a22, …., ann), then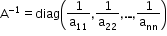
- Type of Square matrices
- Nilpotent Matrix
If for some least +ve integer p, then Ap =0 is a nilpotent matrix.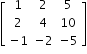
Idempotent Matrix
If A2= A then A is an idempotent matrix.
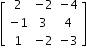
Symmetric Matrix
If AT = A, then A is a symmetric matrix.Skew-symmetric Matrix
If AT = -A, then A is a skew-symmetric matrix.
Also, all the diagonal elements are zero.Involutory Matrix
If A2 = I, then A is an involutory matrix.Unitary Matrix
If A’(A’)T = I, where A’ is the complex conjugate of A, then A is a unitary matrix.Orthogonal Matrix
If A is a square matrix such that ATA = I = ATA or AT = A-1, then A is an orthogonal matrix. - Nilpotent Matrix
- For any square matrix A, A + AT is symmetric and A - AT is skew-symmetric.
- Every square matrix can be expressed as a sum of symmetric and skew-symmetric matrices.
Related Chapters
- Sets, Relations and Functions
- Complex Numbers and Quadratic Equations
- Permutations and Combinations
- Mathematical Induction
- Binomial Theorem and its Simple Applications
- Sequences and Series
- Limit, Continuity and Differentiability
- Integral Calculus
- Differential Equations
- Co-ordinate Geometry
- Three Dimensional Geometry
- Vector Algebra
- Statistics and Probability
- Trigonometry
- Mathematical Reasoning