Rotational Motion

SYNOPSIS

• A rigid body is a solid body of finite size in which deformation is negligible under the effect of deforming forces.
• A rigid body is one in which the distances between different particles of the body do not change.
• The centre of mass (COM) of a rigid body is the point in or near an object at which the whole mass of the object may be considered to be concentrated.
• Collision or impact:
  Collision is an isolated event in which a strong force acts between two or more bodies for a short time which results in a change in their velocities. A rigid object can be substituted with a single particle with mass equal to the total mass of the system located at the COM of the rigid object.
  On the basis of energy, there are two types of collision-elastic collision and inelastic collision.
  On the basis of line of impact, there are two types of collision-head-on collision and oblique collision.
• Conservation of linear momentum: The total momentum of an isolated system remains constant. Momentum is conserved for an isolated system regardless of the nature of internal forces. Law of conservation of linear momentum is independent of the frame of reference.
• In pure translational motion, all particles of the body move with the same velocities in the same direction.
• In pure translational motion, every particle of the body moves with the same velocity at any instant of time.
• In rotational motion, each particle of the body moves along the circular path in a plane perpendicular to the axis of rotation.
• In rotation about a fixed axis, every particle of the rigid body moves in a circle with the same angular velocity at any instant of time.
• Irrespective of where the object is struck, the COM always has translational motion.
• Motion of the COM is the resultant of the motion of all the constituent particles of a system.
• Velocity of the centre of mass of a system of particles is given by
  
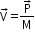
  where is the linear momentum of the system.
• The translational motion of the centre of mass of a system is as if all the mass of the system is concentrated at this point and all the external forces act at this point.
  If the net external force on the system is zero, then the total linear momentum of the system is constant and the centre of mass moves at a constant velocity.
• Torque is the rotational analogue of force in translational motion.
• The torque or moment of force on a system of n particles about the origin is the cross product of radius vectors and force acting on the particles.
  
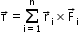
• Angular velocity in rotational motion is analogous to linear velocity in linear motion.
• Conditions for equilibrium:
• The resultant of all the external forces must be zero. The resultant of all the external torques must be zero.
• The centre of gravity is the location in the extended body where we can assume the whole weight of the body to be concentrated.
• When a body acted upon by gravity is supported or balanced at a single point, the centre of gravity is always at and directly above or below the point of suspension.
• The moment of inertia of a rigid body about an axis is defined by the formula 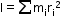, where ri is the perpendicular distance of the ith point of the body from the axis. The kinetic energy of rotation is
  
  
• Theorem of perpendicular axis: The moment of inertia of a planar body (lamina) about an axis perpendicular to its plane is equal to the sum of its moments of inertia about two perpendicular axes concurrent with the perpendicular axis and lying in the plane of the body.
  I = Ix + Iy
  Here,
  Ix: Moment of inertia about the x-axis in the plane of the lamina
  Iy: Moment of inertia about the y-axis in the plane of the lamina
• Theorem of parallel axes: The moment of inertia of a body about any axis is equal to its moment of inertia Icm about a parallel axis through its centre of mass plus the product of the mass M of the body and the square of the distance between the two axes.
  Ip = Icm + Md²
• Work done on a rigid body by an external torque is equal to the change in its kinetic energy.
• Pure rolling implies rolling without slipping. It occurs when there is no relative motion at the point of contact where the rolling object touches the ground.
• For a rolling wheel of radius r which is accelerating, the acceleration of the centre of mass is
• a_cm = Rα
• Law of conservation of angular momentum: If the net resultant external torque acting on an isolated system is zero, then the total angular momentum L of the system should be conserved.
• The relation between the arc length S covered by a particle on a rotating rigid body at a distance r from the axis and the displacement θ in radians is given by S = rθ.