Gravitation
Gravitation PDF Notes, Important Questions and Formulas
INTRODUCTION TO GRAVITATION
Newton observed that an object, an apple, when released near the earth surface is accelerated towards the earth. As acceleration is caused by an unbalanced force, there must be a force pulling objects towards the earth. If someone throws a projectile with some initial velocity, then instead of that object moving off into space in a straight line, it is continuously acted on by a force pulling it back to earth. If we throw the projectile with greater velocity then the path of projectile would be different as well and its range is also increased with initial velocity. If the projection velocity is further increased until at some initial velocity, the body would not hit the earth at all but would go right around it in an orbit. But at any point along its path the projectile would still have a force acting on it pulling it toward the surface of earth. Newton was led to the conclusion that the same force that causes the apple to fall to the earth also causes the moon to be pulled to the earth. Thus the moon moves in its orbit about the earth because it is pulled toward the earth. But if there is a force between the moon and the earth, why not a force between the sun and the earth or why not a force between the sun and the other planets? Newton proposed that the same force, named gravitational force which acts on objects near the earth surface also acts on all the heavenly bodies. He proposed that there was a force of gravitation between each and every mass in the universe.
Newton’s Law of Universal Gravitation
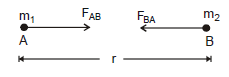
All physical bodies are subjected to the action of the forces of mutual gravitational attraction. The basic law describing the gravitational forces was stated by Sir Issac Newton and it is called Newton's Law. Of Universal gravitation. The law is stated as: "Between any two particles of masses m1 and m2 at separation r from each other there exist attractive forces FAB and FBA directed from one body to the other and equal in magnitude which is directly proportional to the product of the masses of the bodies and inversely proportional to the square of the distance between the two". Thus we can write

Where G is called universal gravitational constant. Its value is equal to 6.67 × 10-11 Nm2/kg. The law of gravitation can be applied to the bodies whose dimensions are small as compared to the separation between the two or when bodies can be treated as point particles.
If the bodies are not very small sized, we cannot directly apply the expression in equation-
(1) to find their natural gravitational attraction. In this case we use the following procedure to find the same. The bodies are initially split into small parts or a large number of point masses.
Now using equation-(1) the force of attraction exerted on a particle of one body by a particle of another body can be obtained. Now we add all forces vectorially which are exerted by all independent particles of second body on the particle of first body. Finally the resultants of these forces is summed over all particles of the first body to obtain the net force experienced by the bodies. In general we use integration or basic summation of these forces.
- Gravitational force is a conservative force.
- Gravitational force is a central force.
- Gravitational force is equal in magnitude & opposite in direction
- Gravitational forces are action - reaction pair.
- Gravitational force acts along the line joining the two masses.
- Gravitational force doesn't depend upon the medium
- Gravitational force is an attractive force.
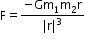
[Head of r is placed at that position where we have to evaluate force]
GRAVITATIONAL FIELD
We can state by Newton's universal law of gravitation that every mass M produces, in the region around it, a physical situation in which, whenever any other mass is placed, force acts on it, is called gravitational field. This field is recognized by the force that the mass M exerts another mass, such as m, brought into the region.
Strength of Gravitational Field
We define gravitational field strength at any point in space to be the gravitational force per unit mass on a test mass (mass brought into the field for experimental observation). Thus for a point in space
if a test mass m0, experiences a force 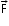 , then at that point in space. Gravitational field strength which F is denoted by
, then at that point in space. Gravitational field strength which F is denoted by 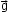 .is given as
.is given as 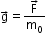
Gravitational field strength y is a vector quantity and has same direction as that of the force on the test mass in field.
Generally magnitude of test mass is very small such that its gravitational field does not modify the field that is being measured. It should be also noted that gravitational field strength is just the acceleration that a unit mass would experience at that point in space.
Gravitational Field Strength of Point Mass
As per our previous discussion we can state that every point mass also produces a gravitational field in its surrounding. To find the gravitational field strength due to a point mass, we put a test mass m0 at a point P at distance x from a point mass m then force on m0 is given as
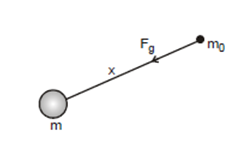
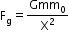
Now if at point P, gravitatioanal field strength due to m is gp then it is given as
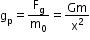
Related Chapters
- Physics and Measurement
- Kinematics
- Laws of Motion
- Work, Energy and Power
- Rotational Motion
- Properties of Solids and Liquids
- Thermodynamics
- Kinetic Theory of Gases
- Oscillations and Waves
- Electrostatics
- Current Electricity
- Magnetic Effects of Current and Magnetism
- Electromagnetic Induction and Alternating Currents
- Electromagnetic Waves
- Optics
- Dual Nature of Matter and Radiation
- Atoms and Nuclei
- Electronic Devices
- Communication Systems

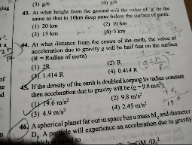


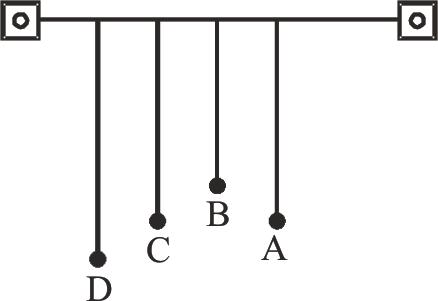 Options:
1.
D will vibrate with maximum amplitude
2.
C will vibrate with maximum amplitude
3.
B will vibrate with maximum amplitude
4.
All the four will oscillate with equal amplitude
Options:
1.
D will vibrate with maximum amplitude
2.
C will vibrate with maximum amplitude
3.
B will vibrate with maximum amplitude
4.
All the four will oscillate with equal amplitude