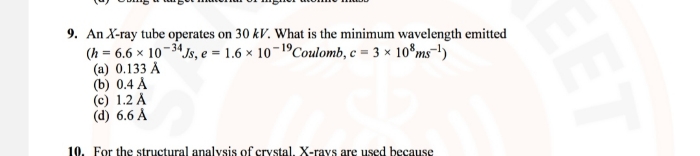Atoms and Nuclei
Atoms and Nuclei PDF Notes, Important Questions and Synopsis
SYNOPSIS
- Thomson’s model of an atom:
An atom consists of positively charged matter in which the negatively charged electrons are uniformly embedded like plums in a pudding. This model could not explain the scattering of α-particles through thin foils and was hence discarded. - Rutherford’s model of an atom:
Geiger and Marsden in their experiment on scattering of a-particles found that most of the a-particles passed undeviated through thin foils, but some of them were scattered through very large angles.
From the results of these experiments, Rutherford proposed the following model of an atom:
- An atom consists of a small and massive central core in which the entire positive charge and almost the whole mass of the atom are concentrated. This core is called the nucleus.
- The nucleus occupies a very small space as compared to the size of the atom.
- The atom is surrounded by a suitable number of electrons so that their total negative charge is equal to the total positive charge on the nucleus and the atom as a whole is electrically neutral.
- The electrons revolve around the nucleus in various orbits just as planets revolve around the sun. The centripetal force required for their revolution is provided by the electrostatic attraction between the electrons and the nucleus. This model could not explain the instability of the atom, because according to the classical electromagnetic theory, the electron revolving around the nucleus must continuously radiate energy in the form of electromagnetic radiation, and hence, it should fall into the nucleus.
- Distance of closest approach:
When an a-particle of mass m and velocity v move directly towards a nucleus of atomic number Z, its initial energy Ei which is just the kinetic energy K gets completely converted to potential energy U at the stopping point. This stopping point happens to be at a distance of the closest approach d from the nucleus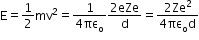
Hence,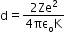
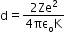
- Bohr’s model for the hydrogen atom:
Basic postulates:
- Nuclear concept: An atom consists of a small massive centre called the nucleus around which planetary electrons revolve. The centripetal force required for their rotation is provided by the electrostatic attraction between the electrons and the nucleus.
- Quantum condition: Of all the possible circular orbits allowed by the classical theory, the electrons are permitted to circulate only in such orbits in which the angular momentum of an electron is an integral multiple of h/2Π, h being Planck’s constant.
where n is called the principal quantum number. - Stationary orbits: While revolving in the permissible orbits, an electron does not radiate energy. These non-radiating orbits are called stationary orbits.
- Frequency condition: An atom can emit or absorb radiation in the form of discrete energy photons only when an electron jumps from a higher orbit to a lower orbit or from a lower orbit to a higher orbit. If E1 and E2 are the energies associated with these permitted orbits, then the frequency ν of the emitted absorbed radiation is given by hυ = E2 − E1
- Radius of the orbit of an electron in the hydrogen atom is
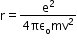
- Potential Energy U
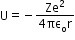
- Total Energy E of the electron in the electron in the hydrogen atom:
E = K + U
- Speed of an electron in the nth orbit is given by
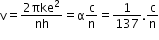
where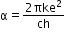
is the fine structure constant.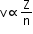 
- Energy of an electron in the nth orbit is given by
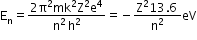
- Spectral series of the hydrogen atom:
Whenever an electron in the hydrogen atom makes a transition from a higher energy level n2 to a lower energy level n1, the difference of energy appears in the form of a photon of frequency v given by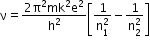
Different spectral series of the hydrogen atom are as follows
- Lyman series: n2 = 2, 3, 4,… and n1 = 1; lies in the ultraviolet region.
- Balmer series: n2 = 3, 4, 5,… and n1 = 2; lies in the visible region.
- Paschen series: n2 = 4, 5, 6,… and n1 = 3; lies in the infrared region.
- Brackett series: n2 = 5, 6, 7,… and n1 = 4; lies in the infrared region.
- Pfund series: n2 = 6, 7, 8,… and n1 = 5; lies in the infrared region.
- Excitation energy:
Energy required by an electron of an atom to jump from its ground state to any one of its excited states - Ionisation energy:
Energy required to remove an electron from an atom, i.e. the energy required to take an electron from its ground state to the outermost orbit (n = ∞). - Excitation potential:
It is that accelerating potential which gives sufficient energy to a bombarding electron so as to excite the target atom by raising one of its electrons from an inner orbit to an outer orbit. - Ionisation potential:
It is the accelerating potential which gives a bombarding electron sufficient energy to move to an outer orbit. - Maser:
Maser stands for ‘Microwaves Amplification by Stimulated Emission of Radiation’. It is a device for producing a highly intense, monochromatic coherent and collimated beam of microwaves. - Laser:
Laser stands for ‘Light Amplification by Stimulated Emission of Radiation’. It is a device used to produce a highly intense strong monochromatic coherent and collimated beam of light. - X-Rays:
X-rays are electromagnetic radiations of very short wavelength and high energy which are emitted when fast-moving electrons or cathode rays strike a target of high atomic mass. X-rays are of two types—characteristic X-rays and continuous X-rays.
Applications of X-rays:
X-rays are used in radio therapy, medicine and surgery. - Moseley's law:
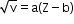
where
V = frequency
a and b = positive constants
Z = atomic number - Atomic number: Number of protons in the nucleus. It is denoted by Z.
- Nuclear mass: Total mass of the protons and neutrons present in a nucleus.
- Isotopes: Atoms of an element which have the same atomic number but different mass number. Isotopes have similar chemical properties but different physical properties.
- Isobars: Atoms with the same mass number but different atomic number.
- Isotones: Nuclides with the same number of neutrons.
- Atomic mass unit: It is
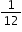th of the actual mass of a carbon atom of isotope 6C12.
It is denoted by amu or just by u.
1 amu = 1.660565 × 10−27 kg
The energy equivalence of 1 amu is
1 amu = 931 MeV - Size of the nucleus: It is found that a nucleus of mass number A has a radius
R = R0A1/3,
where R0 = 1.2 × 10−15 m
This implies that the volume of the nucleus, which is proportional to R3, is proportional to A.
The density of a nucleus is constant and independent of A for all nuclei, and the density of nuclear matter is approximately 2.3 × 1017 kg m−3 which is very large as compared to ordinary matter, say water, which is 103 kg m−3. - Mass defect: The difference between the rest mass of a nucleus and the sum of the rest masses of its constituent nucleons. It is given by
Δm = [Zmp + (A − Z)mn] – m - Binding energy: Energy required to break up a nucleus into its constituent protons and neutrons and to separate them to such a large distance that they may not interact with each other.
It may also be defined as the surplus energy which the nucleus gives up by virtue of their attractions which they become bound together to form a nucleus.
Binding energy of a nucleus zXA is given by
BE = [Zmp + (A − Z)mn – m]c2 - Binding energy per nucleon: It is the average energy required to extract one nucleon from the nucleus. It is obtained by dividing the binding energy of a nucleus by its mass number.
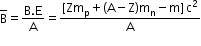
- Nuclear forces: These are the strong attractive forces which hold protons and neutrons together in a tiny nucleus. These are short-range forces which operate over a very short distance of about 2–3 fm of separation between any two nucleons. The nuclear force does not depend on the charge of the nucleon.
- Nuclear density: Density of the nucleus is independent of its size and is given by
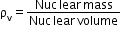
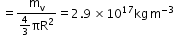
- Radioactivity: The phenomenon of spontaneous disintegration of the nucleus of an atom with the emission of one or more radiations such as α-particles, β-particles or γ-rays. Substances which spontaneously emit penetrating radiation are called radioactive substances.
- Radioactivity displacement law:
- When a radioactive nucleus emits an α-particle, the atomic number decreases by 2 and the mass number decreases by
- When a radioactive nucleus emits a β-particle, the atomic number increases by 1 but the mass number remains the same.
- Emission of a γ-particle does not change the mass number or the atomic number of the radioactive nucleus. γ-particle emission by a radioactive nucleus lowers its energy state.
- Alpha decay: The process of emission of an α-particle from a radioactive nucleus. It may be represented as
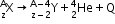
- Beta decay: The process of emission of an electron from a radioactive nucleus. It may be represented as
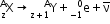
- Gamma decay: The process of emission of a γ-ray photon during the radioactive disintegration of a nucleus. It can be represented as
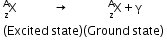
- Radioactive decay law: Number of nuclei undergoing decay per unit time is proportional to the number of undecayed radioactive nuclei present at that instant. It may be written as
N (t) = N (0) e-λt,
where N (0) is the number of nuclei at t = 0 and λ is the disintegration constant. - Decay or disintegration constant: Reciprocal or the time interval in which the number of active nuclei in a given radioactive sample reduces to 36.8%
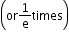of its initial value. - Half-life: Time in which one-half of the nuclei of a radioactive substance will disintegrate. It is inversely proportional to the decay constant of the radioactive substance.
- Mean life: Ratio of the combined age of all the atoms and the total number of atoms in a radioactive sample. It is given by
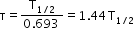
- Nuclear reaction: A reaction which involves the change of stable nuclei of one element into the nucleus of another element.
- Nuclear fission: A process in which a heavy nucleus when excited gets split into two smaller nuclei of nearly comparable masses.
Example: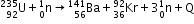
- Nuclear reactor: A device in which a nuclear chain reaction is initiated, maintained and controlled.
- Nuclear fusion: A process of fusion of two smaller nuclei into a heavier nucleus with the liberation of a large amount of energy.
Download complete content for FREE 
NEET - Physics
Asked by roshanrocky334 | 13 Jan, 2024 11:52: AM
ANSWERED BY EXPERTNEET - Physics
Asked by adititiwari601 | 13 Jun, 2022 07:44: AM
ANSWERED BY EXPERTNEET - Physics
Asked by begfatima123 | 06 May, 2022 11:37: PM
ANSWERED BY EXPERTNEET - Physics
Asked by jhajuhi19 | 30 Aug, 2021 08:02: PM
ANSWERED BY EXPERTNEET - Physics
Asked by akshadevdm2020 | 22 May, 2021 03:43: PM
ANSWERED BY EXPERTNEET - Physics
Asked by akdwadasi1111 | 20 Apr, 2021 12:19: PM
ANSWERED BY EXPERTNEET - Physics
Asked by Prashant DIGHE | 10 Apr, 2020 09:21: PM
ANSWERED BY EXPERTRelated Chapters
- Physics and Measurement
- Kinematics
- Laws of Motion
- Work, Energy and Power
- Rotational Motion
- Gravitation
- Properties of Solids and Liquids
- Thermodynamics
- Kinetic Theory of Gases
- Oscillations and Waves
- Electrostatics
- Current Electricity
- Magnetic Effects of Current and Magnetism
- Electromagnetic Induction and Alternating Currents
- Electromagnetic Waves
- Optics
- Dual Nature of Matter and Radiation
- Electronic Devices
- Communication Systems