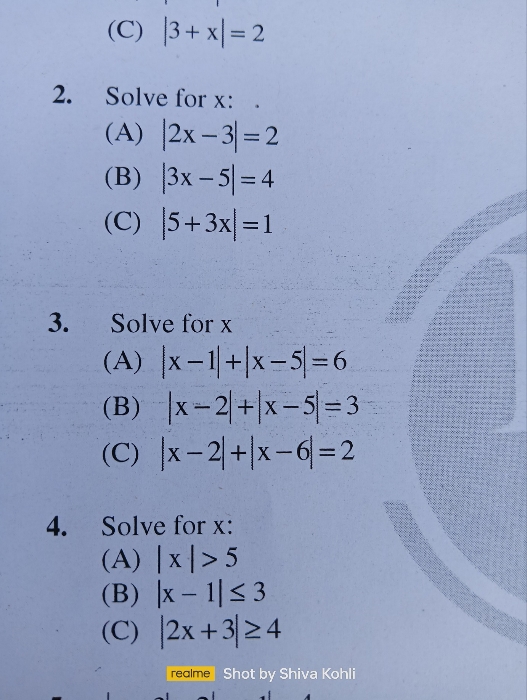Sets, Relations and Functions
Sets, Relations and Functions PDF Notes, Important Questions and Synopsis
SYNOPSIS
- Set:
A set is a well-defined collection of objects and it is denoted by capital letters A, B, ..., Z. - Representation of a set: A set can be represented in two forms:
i. Roster form: All the elements are listed and separated by commas inside the { } braces.
ii. Set builder form: It is the mathematical representation of a set where all the members share a common property listed in the { } braces. - Cardinality of a set: Number of elements present in a set.
- Types of sets:
i. Empty set: A set having no element or cardinality zero is an empty set, i.e. { } or Ø.
ii. Finite set: A set having finite number of elements is a finite set, e.g. A = {1, 2, 3}.
iii. Infinite set: A set having infinite number of elements is an infinite set, e.g. B = {1, 2, 3,...}.
iv. Equal sets: Two sets are equal when they share the same elements and have equal cardinality.
v. Subset: A is a subset of B if B contains all the elements of A.
Note: If A is a subset of B and not equal to B, then A becomes the proper subset of B.
vi. Superset: If B contains all the elements of A, then B is the superset of A.
vii. Power set: The power set of any set A is a set of all the subsets of A and it is denoted by P(A). -
Operations on sets:
i. Disjoint sets: When the sets have no common element, they are called disjoint sets.
ii. Intersection of sets: Intersection of two/more sets is a part (set of elements) which is/are common in those sets (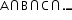 ).
).
iii. Union of sets: Union of two sets A and B is a set containing all the elements of A as well as B.
Same applies for n number of sets ( ).
).
iv.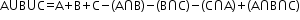
v. Complement of a set: Complement of set A is a set containing all the elements not in A and denoted by A’.
vi. Difference of two sets: Difference of two sets A and B (A⧍B) is a set containing all the elements of A and B which are not common.
vii. Cartesian product of sets: It is a set of ordered pair of elements containing one object from each set.
It is denoted by A × B, where the first object belongs to the first set and the second object belongs to the second set.
Relations
- Relation: A relation R between two sets is a collection of ordered pairs containing one object from each set.
It can also be written as a Cartesian product of two sets, i.e. R = A × B, where all the elements share a common property. -
Types of relations:
i. Reflexive: A relation R is reflexive if ∀ x ∊ X, (x, x) ∊ R.
ii. Symmetric: A relation R is symmetric if (a, b) ∊ R implies (b, a) ∊ R.
iii. Transitive: A relation R is transitive if (a, b) ∊ R and (b, c) ∊ R implies (a, c) ∊ R.
Note: If R is reflexive, symmetric and transitive, then it is an equivalence relation.
iv. Identity: A relation R is an identity if R = {(x, x):x ∊ X}.
Function:
- Function:A function is a relation where each input has a single output.
It is written as f(x), where x is the input. - Domain, Co-domain and Range of a function:
Let f be a function from set A to set B, i.e. f: A→B, then A is the domain and B is the co-domain of f.
Here, all the inputs belong to A and the outputs belong to B.
Set containing all the outputs is the range of a function which is denoted by f(A) = {f(a): a ϵ A}.
Note: Clearly, f(A) ϵ B. - Real-valued function:
A function with domain and range both being subsets of a set of real numbers. -
Operations on functions:
Let f, g: A→B be two real-valued functions, then
i. (f ± g)(x) = f(x)± g(x)
ii. (f • g)(x) = f(x) • g(x)
iii.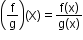 , where g(x)≠0
, where g(x)≠0
Note: Domain for all the above functions is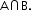
-
Classification of functions:
-
One–one function
A function is a one–one function when each element of domain A is connected with a different element of co-domain B. It is also called injective function.
i.e. For a function f: A→B if "x, y ∊ A such that f(x) = f(y) ⇒ x = y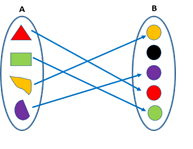
- Many–one function
When any two or more elements of domain A are connected with a single element of co-domain B, then the function is said to be a many–one function.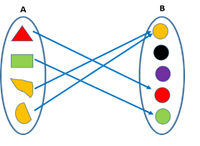
- Onto function
A function f is said to be an onto function if each element of co-domain B is connected with the elements of domain A, i.e. if the range is the same as the co-domain.
It is also called a surjective function.
i.e. f: A→B, "y ∊ B, ∃ x ∊ A such that y = f(x).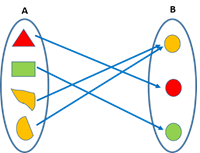
- Into function
A function f is said to be an into function if co-domain B has at least one element which is not connected with any of the elements of domain A.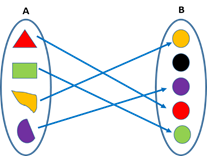
- Bijective function
A function f is said to be a bijective function if it is one–one and onto.
- Types of functions:
Trigonometric functions
Function
Domain
Range
f(x) = sin x
(-∞, +∞)
[−1,1]
f(x) = cos x
(-∞, +∞)
[−1,1]
f(x) = tan x
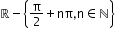
(-∞, +∞)
f(x) = cosec x
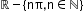
(-∞,-1] U [1, +∞)
f(x) = sec x
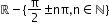
(-∞,-1] U [1, +∞)
f(x) = cot x
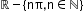
(-∞, +∞)
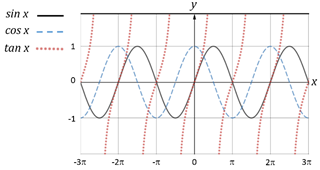
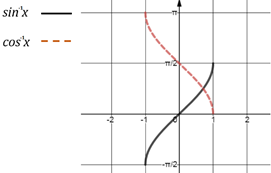
- Inverse trigonometric functions
sin-1x
cos-1x
tan-1x
cot-1x
sec-1x
cosec-1x
Domain
[−1,1]
[−1,1]
(−∞,∞)
(−∞,∞)
(−∞,−1]U[1, ∞)
(−∞,−1]U[1, ∞)
Range
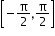
[0,Π]
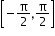
(0,Π)



-
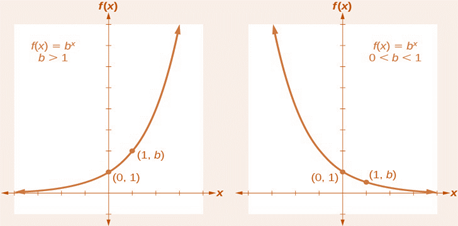
Exponential functions
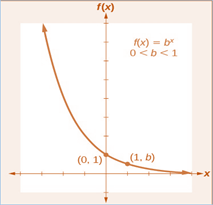
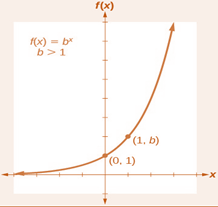
-
Logarithmic functions
-
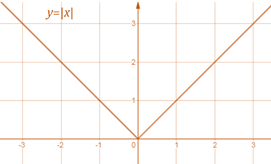
Absolute value function
|x|=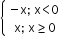
-
Greatest integer function
y=[x]=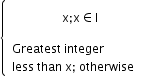
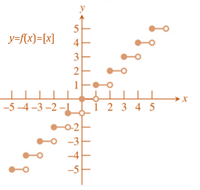
-
Signum function
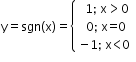

-
Fractional part function

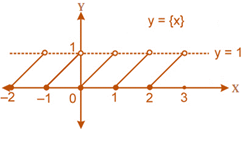
-
Even function
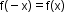 i.e. symmetric about the y-axis
i.e. symmetric about the y-axis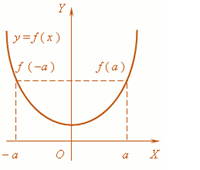
-
Odd function
 i.e. symmetric about the origin
i.e. symmetric about the origin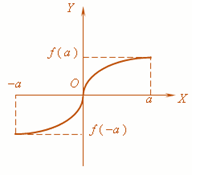
Related Chapters
- Complex Numbers and Quadratic Equations
- Matrices and Determinants
- Permutations and Combinations
- Mathematical Induction
- Binomial Theorem and its Simple Applications
- Sequences and Series
- Limit, Continuity and Differentiability
- Integral Calculus
- Differential Equations
- Co-ordinate Geometry
- Three Dimensional Geometry
- Vector Algebra
- Statistics and Probability
- Trigonometry
- Mathematical Reasoning