Integral Calculus
Integral Calculus PDF Notes, Important Questions and Synopsis
SYNOPSIS
- Integration is the inverse process of differentiation. The process of finding the function from its primitive is known as integration or anti-differentiation.
- Finding a function whenever its derivative is given leads to the indefinite form of integrals.
- Finding the area bounded by a graph of a function under certain conditions leads to the definite form of integrals.
- Indefinite and definite integrals together constitute Integral Calculus.
-
If f(x) is a function, then the family of all its anti-derivatives is called the indefinite integral of f(x) with respect to x.
Indefinite integral, i.e. , where F(x) is the anti-derivative of f(x).
, where F(x) is the anti-derivative of f(x). -
Functions with the same derivatives differ by a constant.
-
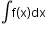 means an integral of f with respect to x, where f(x) is the integrand, x is the variable of integration and C is the constant of integration.
means an integral of f with respect to x, where f(x) is the integrand, x is the variable of integration and C is the constant of integration. -
Geometrically, indefinite integral is the collection of a family of curves, each of which can be obtained by translating one of the curves parallel to itself.
-
Properties of anti-derivatives:
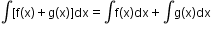
 , for any real number k
, for any real number k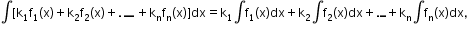 where k1, k2, … kn are real numbers and f1, f2, ... fn are real functions.
where k1, k2, … kn are real numbers and f1, f2, ... fn are real functions. -
Two indefinite integrals with the same derivative lead to the same family of curves and so they are equivalent.
-
Comparison between differentiation and integration:
- Both are operations on functions.
- Both satisfy the property of linearity.
- All functions are not differentiable and all functions are not integrable.
- The derivative of a function is a unique function, but the integral of a function is not unique.
- When a polynomial function P is differentiated, the result is a polynomial whose degree is 1 less than the degree of P. When a polynomial function P is integrated, the result is a polynomial whose degree is 1 more than that of P.
- The derivative of a function is defined at a point P and the integral of a function is defined over an interval.
- Geometrical meaning: The derivative of a function represents the slope of the tangent to the corresponding curve at a point. The indefinite integral of a function represents a family of curves placed parallel to each other having parallel tangents at the points of intersection of the family with the lines perpendicular to the axis.
- A derivative is used for determining certain physical quantities such as the velocity of a moving particle when the distance traversed at any time t is known. Similarly, the integral is used in calculating the distance traversed when the velocity at time t is known.
- Both differentiation and integration are processes involving limits.
- Both are operations on functions.
- Integration can be done using many methods. Prominent among them are
- Integration by substitution
- Integration using partial fractions
- Integration by parts
- Integration using trigonometric identities
-
A change in the variable of integration often reduces an integral to one of the fundamental integrals. Some standard substitutions are
x2 + a2 ; substitute x = a tan θ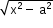 ; substitute x = a sec θ
; substitute x = a sec θ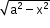 ; substitute x = a sin θ or a cos θ
; substitute x = a sin θ or a cos θ -
A function of the form
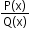 is known as a rational function. Rational functions can be integrated using partial fractions.
is known as a rational function. Rational functions can be integrated using partial fractions. -
Partial fraction decomposition or partial fraction expansion is used to reduce the degree of either the numerator or the denominator of a rational function.
-
Integration using partial fractions:
A rational function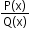 can be expressed as the sum of partial fractions. This takes any of the following forms:
can be expressed as the sum of partial fractions. This takes any of the following forms: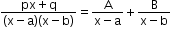 , a ≠ b
, a ≠ b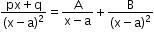


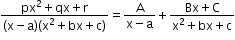 , where
, where 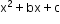 cannot be factorised further.
cannot be factorised further.
-
To find the integral of the product of two functions, integration by parts is used.
I and II functions are chosen using the ILATE rule:
I - Inverse trigonometric
L - Logarithmic
A - Algebraic
T - Trigonometric
E - Exponential
is used to identify the first function. -
Integration by parts:
Integral of the product of two functions = (first function) × (integral of the second function) – integral of [(differential coefficient of the first function) × (integral of the second function)]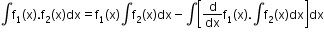 , where f1 and f2 are the functions of x.
, where f1 and f2 are the functions of x. -
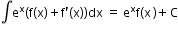
-
Definite integral
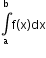 of the function f(x) from limits a to b represents the area enclosed by the graph of the function f(x), the x-axis and the vertical markers x = ‘a’ and x = ‘b’.
of the function f(x) from limits a to b represents the area enclosed by the graph of the function f(x), the x-axis and the vertical markers x = ‘a’ and x = ‘b’.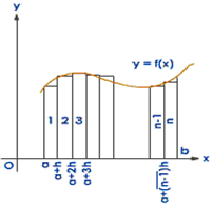
-
Definite integral as the limit of a sum: The process of evaluating a definite integral by using the definition is called integration as the limit of a sum or integration from first principles.
For any function f(x), it is given as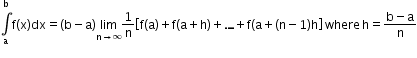
-
Methods of evaluating
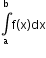
- Calculate anti-derivative F(x)
- Calculate F(b) – F(a)
-
Area function
A(x) =A(x) = , if x is a point in [a, b].
, if x is a point in [a, b].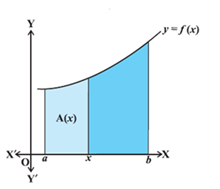
-
Fundamental theorems of integral calculus:
- First fundamental theorem: If area function
A(x) = for all x ≥ a and f is continuous on [a, b], then A′(x) = f(x) for all x Î [a, b].
for all x ≥ a and f is continuous on [a, b], then A′(x) = f(x) for all x Î [a, b]. - Second fundamental theorem: If f is a continuous function of x in the closed interval [a, b] and F is an anti-derivative
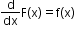 of for all x in domain of f, then
of for all x in domain of f, then
 .
.
Related Chapters
- Sets, Relations and Functions
- Complex Numbers and Quadratic Equations
- Matrices and Determinants
- Permutations and Combinations
- Mathematical Induction
- Binomial Theorem and its Simple Applications
- Sequences and Series
- Limit, Continuity and Differentiability
- Differential Equations
- Co-ordinate Geometry
- Three Dimensional Geometry
- Vector Algebra
- Statistics and Probability
- Trigonometry
- Mathematical Reasoning