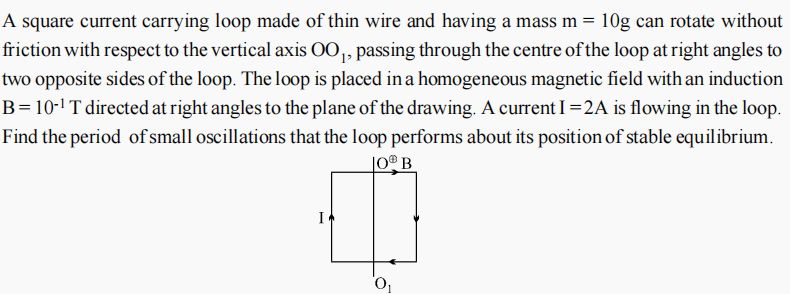
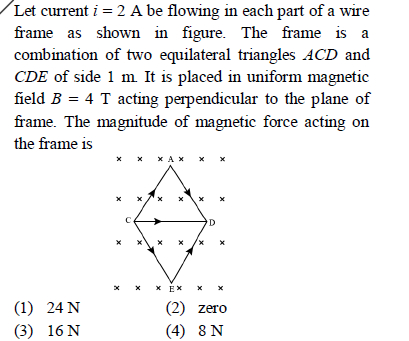
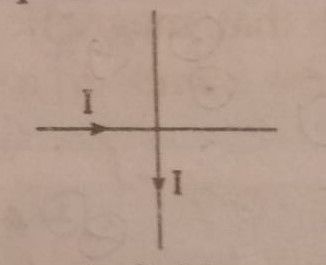
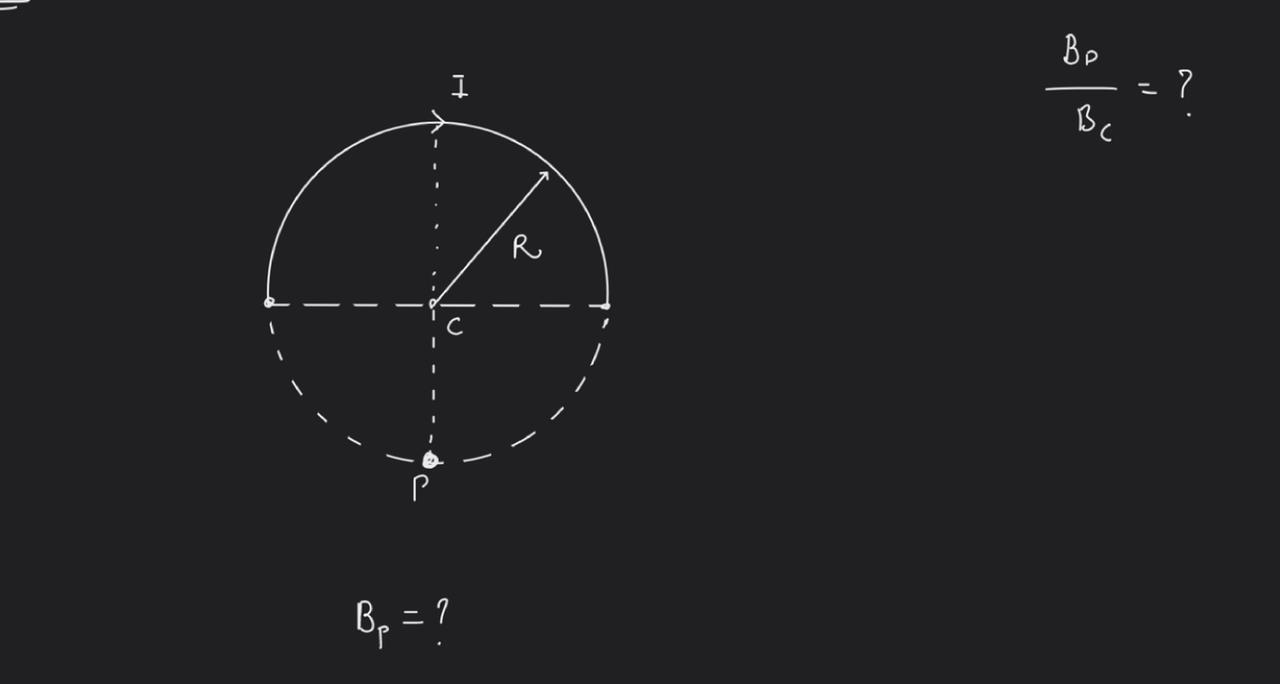
Magnetic Effects of Current and Magnetism

SYNOPSIS

• Lorentz force: Force on a charge q moving with velocity v in the presence of magnetic and electric fields B and E.
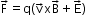
• The magnetic force 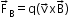is normal to  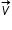and work done by it is zero.
• Force F on a straight conductor of length 𝓁 and carrying a steady current I placed in a uniform external magnetic field B, 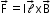 In a uniform magnetic field the force, dF = IBdl Sinθ, does not depend on the position vector r of the current element.Thus, this force is non-central. The force  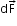is always perpendicular to the plane containing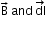 
• Biot–Savart law asserts that the magnetic field 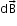 due to an element  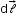carrying a steady current I at a point P at a distance r from the current element is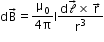
  
  
• The magnetic field due to a circular coil of radius R carrying a current I at an axial distance x from the centre is 
  
  
  
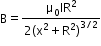
  At the centre of the coil,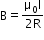
  
  
• Ampere’s circuital law: For an open surface S bounded by a loop C,
  
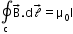   _, where I refers to the current passing through S.
  
  If B is directed along the tangent to every point on the perimeter, then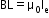
  
  
  Where Ie is the net current enclosed by the closed circuit. Ampere’s law is an important tool in calculating the magnetic field due to current distribution. However, this usefulness is limited to only a few cases where the magnetic field has a symmetrical distribution in space. For example, this law cannot be used to find the magnetic field at the centre of a current-carrying loop. Ampere’s circuital law is not an independent law, but it is derived from Biot–Savart law
  
  
• The magnetic field at a distance R from a long, straight wire carrying a current I is given by
  
  
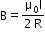
  The field lines are circles concentric with the wire.
  
  
• Magnetic field B inside a long solenoid carrying a current I is
  

  B = μ₀ nI
  where n is the number of turns per unit length.
  For a toriod,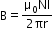
  
  
  
  where N is the total number of turns and r is the average radius.

• Magnetic moment m of a planar loop carrying a current I with N closely wound turns and an area A is
  
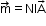
  Direction of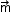  is given by the right-hand thumb rule.
  Right-hand thumb rule: Curl the palm of your right hand along the loop with the fingers pointing in the direction of the current. The thumb sticking out gives the direction of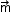  (and  ).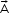
  When this loop is placed in a uniform magnetic field B, the force F on it is F = 0
  and the torque on it is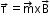 
  In a moving coil galvanometer, this torque is balanced by a counter torque due to a spring yielding
  kϕ = NI AB
  Where ϕ is the equilibrium deflection and k is the torsion constant of the spring.

Uses of a moving coil galvanometer:

• It is used to detect electric current in a circuit, e.g. Wheatstone Bridge.
• It is converted to an ammeter by putting a small resistance parallel to it.
• It is used as an ohmmeter.

• An electron moving around the central nucleus has a magnetic moment 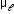 given by
   
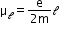
  Where 𝓁 is the magnitude of the angular momentum of the circulating electron about the central nucleus. The smallest value of μ_𝓁 is called the Bohr magneton μ_B, and it is μ_B = 9.27 × 10^–24 J/T.

• Cyclotron:
  A cyclotron is a device used to accelerate positively charged particles (like protons, α-particles, deuterons, ions etc.) to acquire enough energy to carry out nuclear disintegration.
  A charge q executes a circular motion with frequency called the cyclotron frequency given by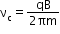
  

  This cyclotron frequency is independent of the particle’s speed and radius.
  Time period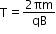
  

  Radius
  
  
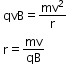
  Limitations of a cyclotron:
  A cyclotron cannot accelerate uncharged particles like neutrons. Positively charged particles with large mass (i.e. ions) cannot be accelerated after a certain speed in the cyclotron.

• Magnetic materials tend to point in the north–south direction.
  Like magnetic poles repel and unlike poles attract each other.
  Cutting a bar magnet in two leads to two smaller magnets.
  Magnetic poles cannot be isolated.

• When a bar magnet of dipole moment 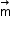 is placed in a uniform magnetic field ,

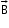• The force on it is zero.
• The torque on it is .
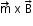• Its potential energy is 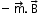, where we choose the zero of the energy at the orientation when is perpendicular to .

• Consider a bar magnet of size 𝓁 nd magnetic moment 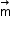 at a distance r from its midpoint, where r >>𝓁; the magnetic field  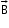due to this bar is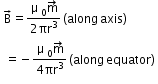
  
  

• Gauss’s law for magnetism: The net magnetic flux through any closed surface is zero.
  
  

• Curie’s law: According to Curie’s law, the susceptibility of a paramagnetic substance is inversely proportional to the absolute temperature: m = c/T, where c is a constant called the Curie constant.

• The pole near the geographic north pole of the Earth is called the north magnetic pole. 
  The pole near the geographic south pole is called the south magnetic pole. 
  The magnitude of the magnetic field on the Earth’s surface = 4 × 10⁻⁵ T.

• Three quantities are needed to specify the magnetic field of the Earth on its surface—the horizontal component, the magnetic declination and the magnetic dip. 
  These are known as the elements of the Earth’s magnetic field.
  
  

• Consider a material placed in an external magnetic field 
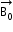
  The magnetic intensity is defined as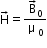
  
  

  The magnetisation 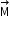 of the material is its dipole moment per unit volume.
  The magnetic field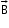  in the material is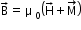
  
  

  For a linear material 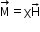 _So,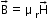
  where
  𝓍: Magnetic susceptibility of the material 
  μ_r: Relative magnetic permeability
  The relative magnetic permeability μr and the magnetic permeability μ are related as follows:

  μ = μ₀ μ_r
  μ_r = 1 +𝓍

• Magnetic materials are broadly classified as diamagnetic, paramagnetic and ferromagnetic. 
  For diamagnetic materials, 𝓍 is negative and small.
  For paramagnetic materials, 𝓍 is positive and small.
  For ferromagnetic materials, 𝓍 is positive and large.

• Substances which at room temperature retain their ferromagnetic property for a long period of time are called permanent magnets.

• HYSTERESIS
  If a ferromagnetic material is magnetised in one direction and the applied magnetising field is removed, then its magnetisation will not be reduced to zero. It must be driven back to zero by a field in the opposite direction. If an alternating magnetic field intensity is applied to the material, its
  magnetisation will trace out a loop called a hysteresis loop. The phenomenon in which magnetic flux density (B) lags behind the magnetising field (H) in a ferromagnetic material during cycles of magnetisation is called hysteresis