Gravitation

SYNOPSIS

• Kepler’s law:
  Law of orbit: Each planet revolves around the sun in an elliptical orbit with the sun at one of the foci.

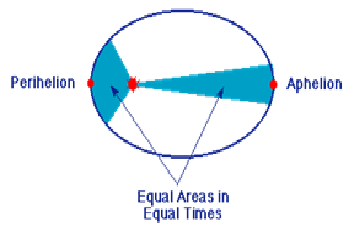
Law of areas: The line joining the sun and the planet sweeps out an equal area in an equal interval of time.

Law of period: The square of the time for a planet to complete a revolution around the sun is proportional to the cube of the semi major axis of the elliptical orbit .

• Newton’s law of gravitation:
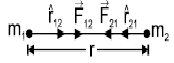
  Every body in the universe attracts every other body with a force which is directly proportional to the product of their masses and inversely proportional to the distance between them. 
  
• Important characteristic of gravitational force:
  Conservative in nature
  Independent of the nature of intervening medium
  Independent of the presence or absence of the other bodies
  Central force

•  Principle of superposition of gravitation: The resultant gravitational force F acting on a particle due to a number of point masses is equal to the vector sum of the forces exerted by the individual masses on the given particle.
  
• Inertial mass and gravitational mass: Inertial mass of the body is related to its inertia of linear motion and is defined by Newton’s second law of motion.

• Gravitational mass: Gravitational mass of a body is related to gravitational pull on the body and is defined by Newton’s law of gravitation.

• Gravitational field:
  The space around a material body in which its gravitational pull can be experienced is called its gravitational field.
  
• Gravity:
  Force of attraction exerted by the earth towards its centre on a body lying on or near the surface of the earth. Force of gravity acting on a body is the measure of the weight of the body.
  
  
• Relation between g and G:
  
• Variation of acceleration due to gravity:
  The value of acceleration due to gravity, i.e.  g changes with height, depth, shape of the earth and rotation of the earth about its own axis. It decreases with height as well as depth.
  Effect of shape: The earth is not a perfect sphere. It is flattened at the poles and bulges out at the equator; thus, the value of g is least at the equator and maximum at the poles.

• Gravitational potential energy:
  The amount of work done in bringing the given body from infinity to that point without acceleration.
   
  Gravitational potential energy = gravitational potential mass of the body
  U = qV

• If an isolated system consists of a particle of mass m moving with a speed v in the vicinity of a massive body of mass M, then the total mechanical energy of the particle is given by
             
• Escape speed:
  The minimum speed required to project a body from the surface of the earth so that it never returns to the surface of the earth is called escape speed. Escape velocity depends on the mass and size of the planet. It is independent of the mass of the body.  ₌ 11.2 km/s
• Energy of an orbiting satellite:
   
  Here, the negative sign shows that the system is bounded.

• Geostationary or geosynchronous satellite:
  A satellite which appears to be at a fixed position at a definite height to an observer on the earth. This satellite revolves around the earth with the same angular speed in the same direction as is done by the earth around its axis.

FORMULAE

GRAVITATION: Universal Law of Gravitation

Where G=6.67×10^­-11Nm²Kg^-2 is the universal gravitational constant.

Newton's Law of Gravitation in vector form:

Now 

Comparing above, we get 

Gravitational Potential: gravitational potential,

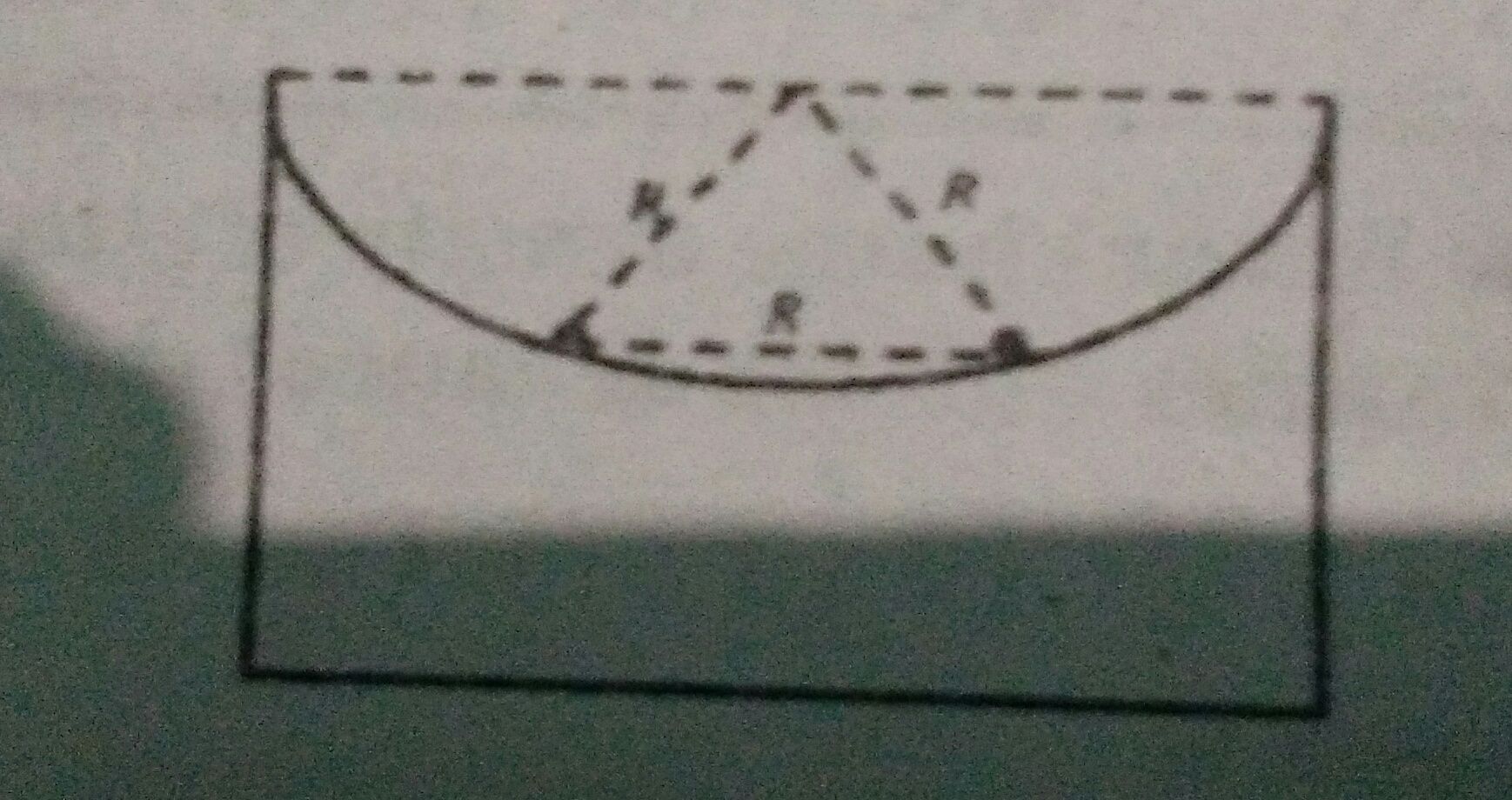
1. Ring.  Or 
   Gravitational field is maximum at a distance,
   r = ∓a/  and it is -2GM/3 a²
2. Thin Circular Disc. 
   
3.   fdfdf
   
   a. Point P inside the sphere. r ≤ a, then
   
   b. Point P outside shell.
   
   
4. Uniform Thin Spherical Shell
   
   a. Point P Inside the shell
   
   b. Point P Outside shell
   
   
   VARIATION OF ACCELERATION DUE TO GRAVITY:

1. Effect of Altitude
   
   
2. Effect of depth 
3. Effect of the surface of Earth
   The equatorial radius is about 21 km longer than its polar radius.
   We know,  
   
   SATELLITE VELOCITY OR ORBITAL VELOCITY
    
   When h<
   
   Time period of Satellite
    
   
   Energy of a Satellite
   
   
4. Kepler’s Laws
   Law of area:
   The line joining the sun and a planet sweeps out equal areas in equal intervals of time.
   
   Law of Periods: