Kinetic Theory of Gases
Kinetic Theory of Gases PDF Notes, Important Questions and Synopsis
SYNOPSIS
- The kinetic theory of gases relates the macroscopic properties of gases such as pressure and temperature to the microscopic properties of gas molecules such as speed and kinetic energy.
- Assumptions of the kinetic theory of gases:
- Collisions between gas molecules or between a molecule and the container are completely elastic.
- Mass of gas molecules is negligible. So, the effect of gravity can be neglected.
- Volume of molecules is considered negligible.
- A collision between molecules is governed by Newton’s Law of Motion (i.e. Net force = Change in momentum per unit time).
- Interaction force between particles is negligible. (That is, they exert no forces on one another.)
- Molecules are considered to be in constant, random and rapid motion. So, average velocity of particles in all the 3-directions will be zero, i.e.=== 0.
- An ideal gas is one in which the pressure p, volume V and temperature T are related by pV = μRT, where R is called the gas constant.
- Real gases satisfy the ideal gas equations only approximately, more so at low pressures and high temperatures.
- The kinetic theory of an ideal gas gives the relation
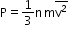
Where n is the number density of molecules, m is the mass of the molecule and is the mean of squared speed. - Root mean square (RMS) speed Vrms: It is defined as the square root of the mean of squares of the speed of different molecules.
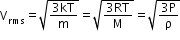
-
The temperature of a gas is a measure of the average kinetic energy of molecules independent of the nature of the gas or molecule. In a mixture of gases at a fixed temperature, the heavier molecules have lower average speedThe pressure exerted by n moles of an ideal gas in terms of the speed of its molecules is P = 1/3 nm vrms2.
-
The average kinetic energy of a molecule is proportional to the absolute temperature of the gas. Molecules of different gases such as
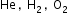 at same temperature will have same translational kinetic energy, though their rms speed is different.
at same temperature will have same translational kinetic energy, though their rms speed is different. -
The degrees of freedom of a gas molecule are independent ways in which the molecule can store energy.
-
Law of equipartition of energy: Every degree of freedom of a molecule has associated with it, on average, an internal energy of (½) kT per molecule.
For f degree of freedom, the equipartition of energy can be given as
Total energy possessed by N molecule = N(f/2)kT
Total energy possessed with each mole = (f/2)RT
Total energy possessed by each molecule = (f/2)kT -
Specific heat of a gas does not have a single or unique value.
In an adiabatic process, the gas is compressed suddenly and no heat is supplied.
Therefore,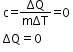
In an isothermal process,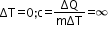
Molar specific heat at constant volume
=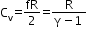
Molar specific heat at constant pressure
=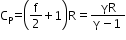
-
Monatomic gases only have three translational degrees of freedom.
-
Diatomic gases in general have three translational, two rotational and two vibrational degrees of freedom.
-
Value of
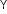 is different for monatomic, diatomic and triatomic molecules.
is different for monatomic, diatomic and triatomic molecules. -
The mean free path is the average distance covered by a molecule between two successive collisions:
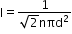 where n is the number density and d is the diameter of the molecule.
where n is the number density and d is the diameter of the molecule. -
If two non-reactive gases are enclosed in a vessel of volume V, where the number of moles of one gas is and another gas is n1 and n2 , then
Total moles =
Molecular weight of mixture
=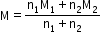
Specific heat of a mixture at constant volume
=
Specific heat of a mixture at constant volume
=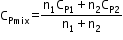
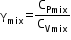
Related Chapters
- Physics and Measurement
- Kinematics
- Laws of Motion
- Work, Energy and Power
- Rotational Motion
- Gravitation
- Properties of Solids and Liquids
- Thermodynamics
- Oscillations and Waves
- Electrostatics
- Current Electricity
- Magnetic Effects of Current and Magnetism
- Electromagnetic Induction and Alternating Currents
- Electromagnetic Waves
- Optics
- Dual Nature of Matter and Radiation
- Atoms and Nuclei
- Electronic Devices
- Communication Systems






