Dual Nature of Matter and Radiation
Dual Nature of Matter and Radiation PDF Notes, Important Questions and Synopsis
SYNOPSIS
An electromagnetic wave has dual (wave–particle) nature.
- The wave nature of light can be observed in the phenomena of interference, diffraction and polarisation.
- While photoelectric effect and Compton effect involve energy and momentum transfer, radiation behaves as if it is made of a bunch of particles-photons show particle nature of a wave.
Wave nature of matter
- De Broglie said that wave nature was symmetrical and that the two basic physical entities—matter and energy-must have symmetrical character. If radiation shows dual aspects, so should matter.
- De Broglie proposed that wavelength λ is associated with a particle of momentum p.
- This wavelength is so small that it is beyond any measurement. This is the reason why macroscopic objects in daily life do not show wave-like properties.
- De Broglie hypothesis
- Matter shows dual character like electromagnetic radiation does. It also shows wave-like properties.
- Apart from being a particle, a wavelength associated with matter is called de Broglie
wavelength. It is given by the relation,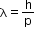
- where m is the mass of the particle, v is speed and h is Planck’s constant.
- On the left-hand side of the above equation, λ is the attribute of a wave, while on the right-hand side, the momentum p is a typical attribute of a particle.
- De Broglie wavelength for a photon
- De Broglie’s idea that matter also exhibits duality and has wave properties can be expressed quantitatively by first considering electromagnetic radiation.
- A photon of frequency v and wavelength λ has energy:

- De Broglie wavelength for an electron
If an electron (charge = e) is accelerated by potential difference of volts, then it acquires kinetic energy of
K=eV - Therefore, the formula can be written as
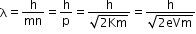
- Substituting the numerical values of h, m and e,
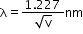
Davison and Germer experiment
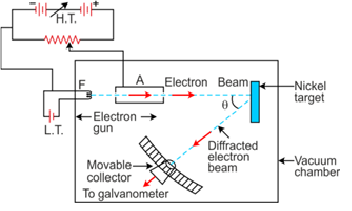
Davisson–Germer electron diffraction arrangement
Result
-
It was noticed that a strong peak appeared in the intensity (I) of the scattered electron for an accelerating voltage of 54 V at a scattering angle θ = 50°.
-
This is due to the constructive interference of electrons scattered from different layers of the regularly spaced atoms of the crystals.
-
From the electron diffraction measurements, the wavelength of matter waves was found to be 0.165 nm.
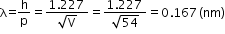
Photoelectric effect
- When light falls on a metal surface, some electrons near the surface absorb enough energy from the incident radiation to overcome the attraction of the positive ions in the material of the surface.
- After gaining sufficient energy from the incident light, the electrons escape from the surface of the metal into the surrounding space.
- The photoelectric emission is an instantaneous process without any apparent time lag (〖~10〗^(-9)s or less) even when the incident radiation is made exceedingly dim.
Photoelectric effect
- When light of an appropriate frequency (or correspondingly of an appropriate wavelength) is incident on a metallic surface, electrons are liberated from the surface. These photo- or light-generated electrons are called photoelectrons.
- The incident light photon should be greater than or equal to the work function of the metal.
E ≥ W
hν ≥ W
ν ≥ W/h
Work function
- The minimum energy required by an electron to escape from the metal surface is called the work function of the metal. It is generally denoted by W and measured in electron volt (eV).
Threshold frequency
- The minimum frequency W/h required for emission of electrons is called threshold frequency. It is denoted by ν0.
ν0 = W/h (threshold frequency)
Effect of intensity of light on photocurrent
- Photocurrent increases linearly with the intensity of incident light when accelerating potential is fixed.
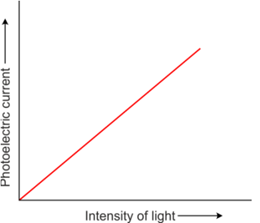
Effect of potential on photoelectric current
- The photoelectric current increases with an increase in accelerating (positive) potential.
- The maximum value of the photoelectric current is called saturation current.
- At saturation current, all the photoelectrons emitted by the emitter plate reach the collector plate.
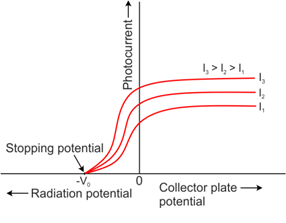
Intensity of incident radiation
- The photocurrent is found to decrease rapidly until it drops to zero at a certain critical value of the negative potential V0, which is called the retarding potential V0.
- The minimum negative (retarding) potential given to the plate for which the photocurrent stops or becomes zero is called the cut-off or stopping potential.
- Photoelectric current is zero when the stopping potential is sufficient to repel even the most energetic photoelectrons with the maximum kinetic energy (Kmax).
K max = e V0
Einstein’s photoelectric equation
- The electron is emitted with maximum kinetic energy given by K max = hν – φ0.
- Kmax depends linearly on ν and is independent of the intensity of radiation.
- Photoelectric emission is possible only if h ν > φ0.
- Greater the work function φ0, higher the minimum or threshold frequency ν0 needed to emit photoelectrons.
Photoelectric equation can be written as eV0 = h ν – φ0, for ν ≥ ν0.
Related Chapters
- Physics and Measurement
- Kinematics
- Laws of Motion
- Work, Energy and Power
- Rotational Motion
- Gravitation
- Properties of Solids and Liquids
- Thermodynamics
- Kinetic Theory of Gases
- Oscillations and Waves
- Electrostatics
- Current Electricity
- Magnetic Effects of Current and Magnetism
- Electromagnetic Induction and Alternating Currents
- Electromagnetic Waves
- Optics
- Atoms and Nuclei
- Electronic Devices
- Communication Systems


