Electromagnetic Induction and Alternating Currents
Electromagnetic Induction and Alternating Currents PDF Notes, Important Questions and Synopsis
SYNOPSIS
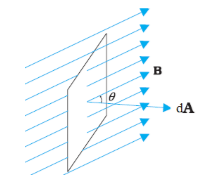
Magnetic flux
Magnetic flux through a plane of area dA placed in a uniform magnetic field B
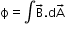
If the surface is closed, then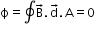
This is because magnetic lines of force are closed lines and free magnetic poles do not exist.
Electromagnetic Induction: Faraday’s Law
- First law: Whenever there is a change in the magnetic flux linked with a circuit with time, an induced emf is produced in the circuit which lasts as long as the change in the magnetic flux continues.
- Second law: The induced emf is equal to negative of the rate of change of flux through the circuit.
Induced emf,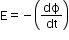
Lenz’s Law
The direction of the induced emf or current in the circuit is such that it opposes the cause by which it is produced, so that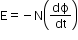
N → Number of turns in the coil
Lenz’s law is based on energy conservation
Fleming’s right-hand rule: It states that if the thumb and the first two fingers of the right hand are stretched mutually perpendicular to each other and if the forefinger gives the direction of the magnetic field and the thumb gives the direction of motion of the conductor, then the central finger gives the direction of the induced current.
Emf, current and charge induced in the circuit
- Induced emf
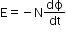
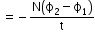
- Induced current
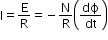
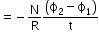
Charge depends only on net change in flux and does not depend on time.
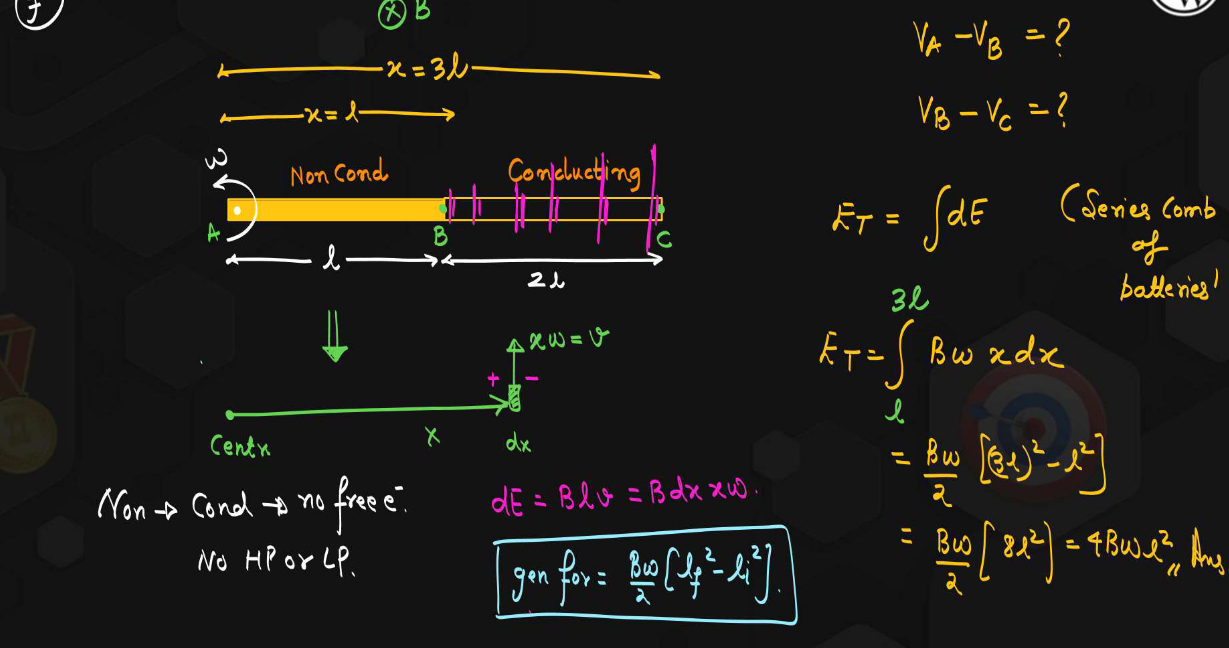
Emf induced due to linear motion of a conducting rod in a uniform magnetic field
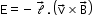
If 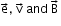 are perpendicular to each other, then
are perpendicular to each other, then
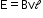
Induced emf due to rotation of a conducting rod in a uniform magnetic field
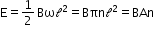
where n is the frequency of rotation of the conducting rod.
Direction of emf is given by the right-hand thumb rule.
Induced emf due to rotation of a metallic disc in a uniform magnetic field
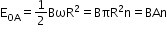
Induced emf, current and energy conservation in a rectangular loop moving in a non-uniform magnetic field with a constant velocity
- Net increase in flux crossing through the coil in time Δt
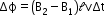
- Emf induced in the coil
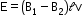
- If the resistance of the coil is R, then the current induced in the coil is

- Resultant force acting on the coil
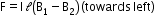
- Work done against the resultant force
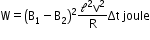
Energy supplied in this process appears in the form of heat energy in the circuit. - Energy supplied due to flow of current I in time Δt
H = I²R Δt
Or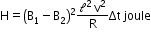
Or H = W
Rotation of a rectangular coil in a uniform magnetic field
- Magnetic flux linked with the coil
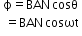
- Emf induced in the coil
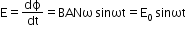
- Current induced in the coil
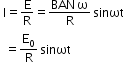
- Both emf and current induced in the coil are alternating.
Self-induction and self-inductance (L)
When an induced emf is produced in the coil on changing the current in a coil, the phenomenon is called self-induction.

or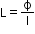
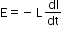
where L is a constant called self-inductance or coefficient of self-induction.
or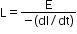
- Self-inductance of a circular coil
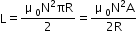
- Self-inductance of a solenoid
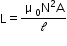
- Two coils of self-inductances L1 and L2placed far away (i.e. without coupling) from each other.
- For a series combination:
L = L1 + L2 … Ln - For a parallel combination:
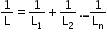
- For a series combination:
Mutual induction and mutual inductance
- On changing the current in one coil, if the magnetic flux linked with a second coil changes and an induced emf is produced in that coil, then this phenomenon is called mutual induction.

Or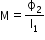

Or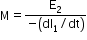
- M12 = M21 = M
- Mutual inductance of two coaxial solenoids
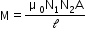
- If two coils of self-inductance L1 and L2 are wound over each other, then the mutual inductance is given by
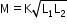
Where K is called the coupling constant. - For two coils wound in the same direction and connected in series,
L = L1 + L2 + 2M
For two coils wound in the opposite direction and connected in series,
L = L1 + L2 – 2M
For two coils in parallel,
Energy stored in an inductor
Energy stored in the form of Magnetic Field
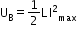
Magnetic energy density

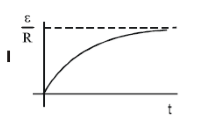
Growth of current in series LR circuit
If a circuit consists of a cell, an inductor L, a resistor R and a switch S connected in series, and the switch is closed at t = 0, the current in the circuit I will increase as 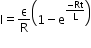
The quantity L/R is called the time constant of the circuit and is denoted by τ. The variation of current with time is as shown.
- Final current in the circuit=
 , which is independent of L.
, which is independent of L. - After one time constant, current in the circuit is 63% of the maximum value of current.
Decay of current in the circuit containing resistor and inductor:
Let the initial current in a circuit containing inductor and resistor be I0.
Current at time t is given as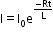
Current after one time constant: I = I0e-1 = 0.37% of initial current
The time constant τ is defined as the time interval during which the current decays to 37% of the
maximum current during decay. The rate of decay of the current shows an exponential decay behaviour.
Eddy current
When a conductor is moved in a magnetic field, induced currents are generated in the whole volume of the conductor. These currents are called eddy currents.
Oscillating LC circuit
If a charged capacitor C is short circuited through an inductor L, the charge and current in the circuit start oscillating simple harmonically. If the resistance of the circuit is zero, no energy is dissipated as heat. We also assume an idealised situation in which energy is not radiated away from the circuit. With these idealisations—zero resistance and no radiation—the oscillations in the circuit persist indefinitely and the energy is transferred from the capacitor’s electric field to the inductor’s magnetic field and back.
The total energy associated with the circuit is constant. This is analogous to the transfer of energy in man oscillating mechanical system from potential energy to kinetic energy and back, with constant total energy. Charge in the circuit oscillates simple harmonically with angular frequency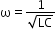
Transformer- It is a device which changes the magnitude of alternating voltage or current.
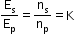
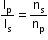 (for ideal transformer)
(for ideal transformer)- In an ideal transformer:
EpIp = EsIs or Pin = Pout - In a step-up transformer:
ns > np or K > 1
Es > Ep and Is < Ip - In a step-down transformer:
ns < np or K < 1
Es < Ep and Is > Ip - Efficiency

- It is a device which changes the magnitude of alternating voltage or current.
Generator or dynamo
It is a device by which mechanical energy is converted to electrical energy. It is based on the principle of EMI.
AC Generator
In an AC generator, mechanical energy is converted to electrical energy by virtue of electromagnetic induction. It consists of a field magnet, armature, slip rings and brushes. If the coil of N turns and area A is rotated at 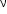 revolution per second in a uniform magnetic field B, then the motional emf produced is
revolution per second in a uniform magnetic field B, then the motional emf produced is 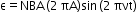 , where we have assumed that at time t = 0 s, the coil is perpendicular to the field.
, where we have assumed that at time t = 0 s, the coil is perpendicular to the field.
Alternating current (AC)
The current whose magnitude changes with time and direction reverses periodically is called alternating current.
- Alternating emf E and current I at any time are given by
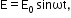 where E0 = NBA ω
where E0 = NBA ω
and I = I0 sin (ωt − ϕ); here, I0 = NBA ω/R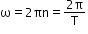 ,T → Time period
,T → Time period
Values of alternating current and voltage
- Instantaneous value: It is the value of alternating current and voltage at an instant t.
- Peak value: Maximum values of voltage E0 and current I0 in a cycle are called peak values.
- Mean value: For a complete cycle,
< E > =
< I > =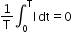
Mean value for a half cycle: Emean=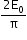
- Root mean square (rms) value:
Erms = (< E2 >)½ =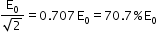
and Irms (< I2 >)½ =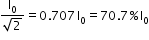
RMS values are also called apparent or effective values.
Phase difference between emf (Voltage) and current in an AC circuit
- For pure resistance: Voltage and current are in the same phase, i.e. phase difference = 0.
- For pure inductance: Voltage is ahead of current by π/2, i.e. phase difference = +π/2.
- For pure capacitance: Voltage lags behind current by π/2, i.e. phase difference = −π/2.
Reactance
- Reactance
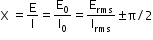
- Inductive reactance
XL =ωL = 2πnL - Capacitive reactance
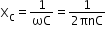
Impedance
- Impedance Z =
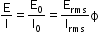
where ϕ is the phase difference of the voltage E relative to the current I. - For L–R series circuit:
ZRL =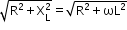
and tan ϕ =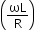 or
or 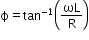
- For R–C series circuit:
ZRC =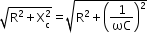
and tanϕ =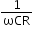 or
or 
- For L–C–R series circuit:
ZLCR =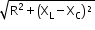
=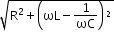
and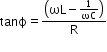 Or
Or 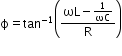
Conductance
The reciprocal of resistance is called conductance.
∴ Conductance 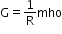
Power in an AC circuit
- Electric power = (current in circuit) × (voltage in circuit)
P = IE - Instantaneous power:
Pinst = Einst × Iinst - Average power:
Pav =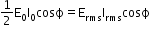
- Virtual power (apparent power):
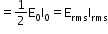
Power factor
- Power factor
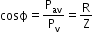
- For pure inductance:
Power factor,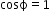
- For pure inductance:
Power factor,
- For LCR circuit:
Power factor,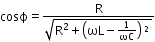
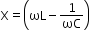
Wattless current
The component of current whose contribution to the average power is nil is called wattless current.
RMS value of wattless current:
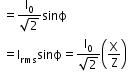
Choke coil
An inductive coil used for controlling the alternating current whose self-inductance is high and resistance in negligible is called a choke coil.
The power factor of this coil is given by
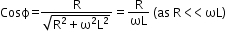
Now, as we know that 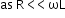 , the power factor is small, and hence, the power absorbed will be very small. Also, on account of its large impedance (large inductance), current passing through the
, the power factor is small, and hence, the power absorbed will be very small. Also, on account of its large impedance (large inductance), current passing through the
coil is very small. Hence, such a coil is preferred in electrical circuits for the purpose of adjusting the current to any desired value without significant energy waste.
Series resonant circuit
- When the inductive reactance (XL) becomes equal to the capacitive reactance (XC) in the circuit, the total impedance becomes purely resistive (Z = R). In this state, the voltage and current are in the same phase (ϕ= 0), the current and power are maximum and the impedance is minimum. This state is called resonance.
- At resonance,
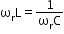
Hence, resonant frequency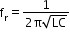
- In resonance, the power factor of the circuit is one.
Half-power frequencies
Frequencies f1 and f2 at which the power is half of the maximum power (power at resonance), i.e.
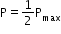 and
and  are called half-power frequencies.
are called half-power frequencies.
Bandwidth
The frequency interval between half-power frequencies is called bandwidth.
∴ Bandwidth Δf = f2 – f1
For a series LCR resonant circuit,
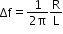
Quality factor (Q)
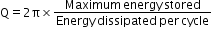
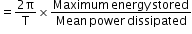
Or 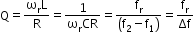
Related Chapters
- Physics and Measurement
- Kinematics
- Laws of Motion
- Work, Energy and Power
- Rotational Motion
- Gravitation
- Properties of Solids and Liquids
- Thermodynamics
- Kinetic Theory of Gases
- Oscillations and Waves
- Electrostatics
- Current Electricity
- Magnetic Effects of Current and Magnetism
- Electromagnetic Waves
- Optics
- Dual Nature of Matter and Radiation
- Atoms and Nuclei
- Electronic Devices
- Communication Systems