Differential Equations
Differential Equations PDF Notes, Important Questions and Synopsis
SYNOPSIS
- An equation involving derivatives of a dependent variable with respect to an independent variable is called a differential equation.
Example: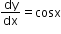 ,
, 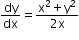
-
The order of a differential equation is the number of the highest order derivative occurring in the differential equation.
Example: Order of the differential equation
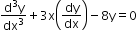 .
. -
The degree of a differential equation is the highest power (exponent) of the highest order derivative in it when it is written as a polynomial in differential coefficients.
Degree of equation
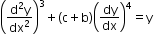 is 3.
is 3. -
The order and the degree of a differential equation are positive integers.
-
A differential equation is a linear differential equation if it is expressed in the form:
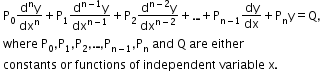
-
A differential equation will be a non-linear differential equation if
- Its degree is more than one.
- The exponent of any differential equation is more than one.
- The exponent of the dependent variable is more than one.
- The products containing the dependent variable and its differential coefficients are present.
-
A function which satisfies a given differential equation is called its solution.
-
To formulate a differential equation:
- Consider an equation involving an independent variable, dependent variable and constants.
- Determine the number of constants and assume there be 'n' arbitrary constants.
- Differentiate the relation n times with respect to x, where n is number of arbitrary constants.
-
The solution which contains as many arbitrary constants as the order of the differential equation is called a general solution.
-
The solution which is free from arbitrary constants is called a particular solution.
-
The order of a differential equation is equal to the number of arbitrary constants present in the general solution.
-
An nth order differential equation represents an n-parameter family of curves.
-
Three methods of solving first-order and first-degree differential equations:
- Separating the variables if the variables can be separable.
- Substitution if the equation is homogeneous.
- Using an integrating factor if the equation is a linear differential equation.
-
The variable separable method is used to solve equations in which variables can be separated, i.e. the terms containing y should remain with dy and the terms containing x should remain with dx.
-
The solution of the differential equation
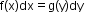 , which is in the variable separable form, is given by
, which is in the variable separable form, is given by .
. -
A differential equation of the form
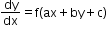 can be reduced to the variable separable form by substituting ax + by + c = v.
can be reduced to the variable separable form by substituting ax + by + c = v. -
A differential equation which can be expressed in the form
 = f(x, y) or
= f(x, y) or 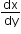 = g(x, y), where f(x, y) and g(x, y) are homogeneous functions, is called a homogeneous differential equation.
= g(x, y), where f(x, y) and g(x, y) are homogeneous functions, is called a homogeneous differential equation. -
The degree of each term is the same in a homogeneous differential equation.
-
Homogeneous equations can be reduced to the variable separable form by the substitution of y = vx or x = vy.
-
Steps to solve a homogeneous differential equation:
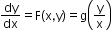 … (1)
… (1)
Substitute y = v.x … (2)
Differentiate (2) with respect to x
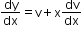 … (3)
… (3)
Substitute and separate the variables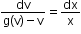
Integrate
-
A differential equation of the form
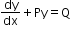 , where P and Q are constants or functions of x only, is called a first-order linear differential equation.
, where P and Q are constants or functions of x only, is called a first-order linear differential equation.
OR
A differential equation of the form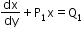 , where P1 and Q1 are constants or functions of y only, is called a first-order linear differential equation.
, where P1 and Q1 are constants or functions of y only, is called a first-order linear differential equation. -
Solution of
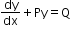 , where P and Q are constants or functions of x:
, where P and Q are constants or functions of x:
Integrating factor (IF) = e ∫Pdx
Solution: y (IF) = ∫ (Q × IF)dx + C -
Solution of
 , where P1 and Q1 are constants or functions of y:
, where P1 and Q1 are constants or functions of y:
Integrating factor (IF) = e ∫P1dy
Solution: x (IF) = ∫ (Q1 × IF)dy + C
Related Chapters
- Sets, Relations and Functions
- Complex Numbers and Quadratic Equations
- Matrices and Determinants
- Permutations and Combinations
- Mathematical Induction
- Binomial Theorem and its Simple Applications
- Sequences and Series
- Limit, Continuity and Differentiability
- Integral Calculus
- Co-ordinate Geometry
- Three Dimensional Geometry
- Vector Algebra
- Statistics and Probability
- Trigonometry
- Mathematical Reasoning



