Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 12-science Answered

Four particles each of mass mass charge q are held at the vertices of a square of side a. They are released at t=0 and move under mutual repulsive forces. Find the speed of any paticle when its distance from the centre of the square is double.
Asked by Archit | 31 May, 2015, 07:14: PM
answered-by-expert Expert Answer
begin mathsize 12px style Four space particles space each space of space mass space mass space charge space straight q space are space held space at space the space vertices space of space straight a space square space of space side space straight a. space To space find space the space speed space of space any space paticle space we space need space to space figure space out space intial space potential space energy space and space final space potential space energy space when space the space distance space of space square space is space double. Total space potential space energy space is space given space as comma increment straight U equals straight U subscript straight i minus straight U subscript straight f straight U subscript straight i equals Kq squared open square brackets 4 over straight a plus fraction numerator 2 over denominator square root of 2 straight a end fraction close square brackets straight U subscript straight f equals Kq squared open square brackets fraction numerator 4 over denominator 2 straight a end fraction plus fraction numerator 2 over denominator square root of 2 left parenthesis 2 straight a right parenthesis end fraction close square brackets From space the space figure space we space have space four space side space of space square space and space two space side space across space digonal space hence comma increment straight U equals Kq squared open square brackets 4 over straight a plus fraction numerator 2 over denominator square root of 2 straight a end fraction close square brackets minus Kq squared open square brackets fraction numerator 4 over denominator 2 straight a end fraction plus fraction numerator 2 over denominator square root of 2 left parenthesis 2 straight a right parenthesis end fraction close square brackets space space space space space space space space equals Kq squared open square brackets 4 over straight a plus fraction numerator 2 over denominator square root of 2 straight a end fraction minus fraction numerator 4 over denominator 2 straight a end fraction minus fraction numerator 2 over denominator square root of 2 left parenthesis 2 straight a right parenthesis end fraction close square brackets increment straight U equals Kq squared open square brackets 2 over straight a plus fraction numerator 1 over denominator square root of 2 straight a end fraction close square brackets To space find space the space speed space of space any space particle space we space need space to space divide space potential space energy space by space 4. since space potential space enegy space loss space by space 4 space charges. By space the space conservation space of space energy space loss space in space potential space energy space is space equal space to space kinetic space energy. 1 fourth Kq squared open square brackets 2 over straight a plus fraction numerator 1 over denominator square root of 2 straight a end fraction close square brackets equals 1 half mv squared straight v squared equals Kq squared over straight m open square brackets 2 over straight a plus fraction numerator 1 over denominator square root of 2 straight a end fraction close square brackets The space velocity space of space any space particle space will space be comma straight v equals square root of Kq squared over straight m open square brackets 2 over straight a plus fraction numerator 1 over denominator square root of 2 straight a end fraction close square brackets end root end style
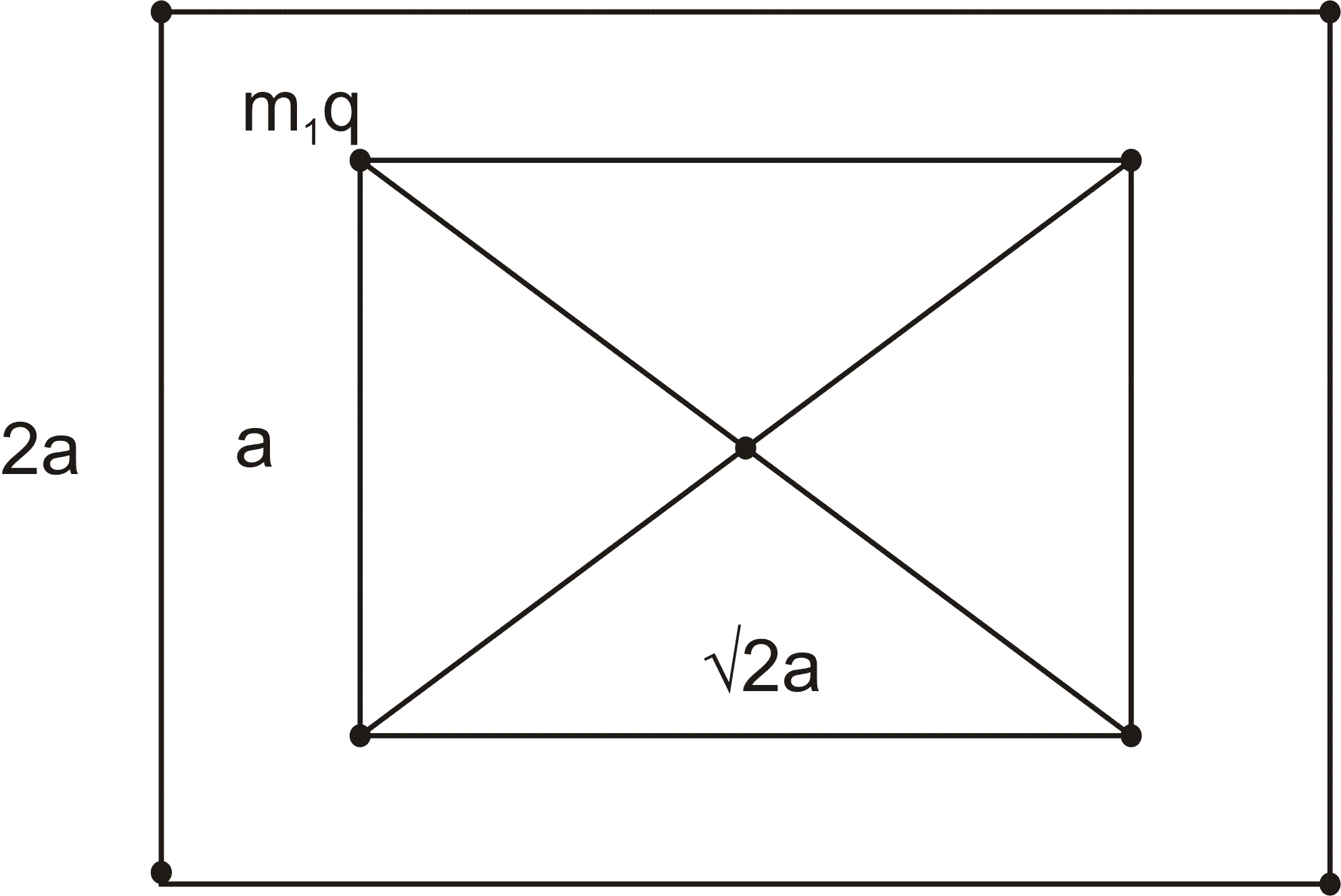
Answered by Priyanka Kumbhar | 01 Jun, 2015, 03:00: PM

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 12-science - Physics
if breakdown voltage of each capacitor is 40v ,then maximum applied voltage Vmax will be
Asked by aishaisha091098 | 19 Apr, 2024, 04:54: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
solve option e
question image
Asked by dasrituparna1999 | 13 Apr, 2024, 06:56: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
A parallel-plate capacitor has a plate area of 100c * m ^ 2 and a plate separation of 2.0 cm. has been charged up to 3000 V by a battery. Now, (i) after disconnecting the battery, (ii) keeping the battery connected, the distance between the plates is increased to 5.0 cm intensity of electric field between the plates and the energy of the capacitor. ( epsilon_{0} = 8.85 * 10 ^ - 12 * F * m ^ - 1
Asked by khankaifi178 | 08 Jan, 2024, 10:12: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
  A particle with charge q and mass m is released just outside the centre of a uniformly charged square plate of side a and potential V.find the speed in which the particle files off away from the plate
Asked by sankaraganapathy007 | 09 Sep, 2023, 10:03: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
obtain expression for force between plates of a charged parallel plate capacitor
Asked by bmahalik21 | 05 Mar, 2023, 08:23: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
What is capacitance
Asked by s3043632 | 22 Jan, 2023, 06:45: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
a conducting sphere is charged upto 2 uc. if the radius of sphere is 10 cm, then the electric field due to this charged system, at 5 cm from the centre of sphere, will be
Asked by carnivalgirl8421 | 29 Jun, 2022, 11:18: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
what is the dielectric
Asked by priyr7687 | 28 Jun, 2022, 06:19: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
the work done is moving charge of 2c across two point having a potential difference of 12volt
Asked by tahseenaamir07 | 25 Jun, 2022, 01:33: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
hello
question image
Asked by ekanathtanpure77 | 23 Jun, 2022, 07:56: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×