Sequence and Series

Synopsis

1. Introduction to Sequence
   • A sequence is an ordered list of numbers and has the same meaning as in conversational English.
   • A sequence is denoted by <a_n> (n ≥ 1) = a₁, a₂, a₃, …….a_n
   • The various numbers occurring in a sequence are called its terms.
   • The n^th term <a_n> is called the general term of the sequence.
   • The expression obtained by adding all the terms of a sequence is called the series associated with the given sequence.
   
   
2. Finite and Infinite sequences
   • A sequence containing finite number of terms is called a finite sequence. A finite sequence has a last term
   • A sequence which is not a finite sequence, i.e. containing infinite number of terms is called an infinite sequence. There is no last term in an infinite sequence.
    
3. Fibonacci sequence
   Fibonacci sequence 1, 1, 2, 3, 5, 8,… is generated by the recurrence relation given by
   a₁ = a₂ = 1
   a₃ = a₁ + a₂……
   a_n = a_n-2 + a_n-1, n > 2
    
4. Arithmetic Progression
   • A sequence is said to be an arithmetic progression or A.P., if every term differs from the preceding term by a constant number.
   • For example, sequence a₁, a₂, a₃,… a_n is called an arithmetic sequence or an A.P.  If a_n+1 = a_n + d, for all n ε N, where ‘d’ is a constant called the common difference of the A.P.
   
   • General term of an A.P.
   i. The n^th term or general term of an A.P. is a_n = a + (n – 1)d, where a is the first term and d is the common difference.
   ii. General term of an A.P., given its last term ‘λ’ is λ – (n – 1)d.
   iii. General form of an A.P. is a, a + d, a + 2d,… a + (n - 1)d. ‘a’ is called the first term of the A.P. and ‘d’ is called the common difference of the A.P. ‘d’ can be any real number.
   iv. Let ‘a’ be the first term and ‘d’ be the common difference of an A.P. with 'm' terms. Then the n^th term from the end is the (m – n + 1)^th term from the beginning.
   
   • Sum of n terms of an A.P.
   i. Let a, a + d, a + 2d, …, a + (n – 1)d be an A.P.
   Then,  where 𝓁 = a + (n – 1) d
   ii. A sequence is an A.P. if and only if the sum of its n terms is an expression of the form Xn² + Yn, where X and Y are constants.
   
   • Arithmetic Mean
   i. ‘A’ is the arithmetic mean of two numbers ‘a’ and ‘b’ if a, A and b form an arithmetic progression and it is given by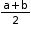 
   ii. Let A₁, A₂, A₃, … A_n be n numbers between a and b such that a, A₁, A₂, A₃, …An, b is an A.P.
   These n numbers between a and b are as follows:
   
   
   • Nature of A.P. depending upon the common difference d
   i. If d > 0 then the A.P. is increasing.
   ii. If d < 0 then the A.P. is decreasing.
   iii. If d = 0 then the A.P. is constant.
   
   • Selection of Terms
   i. If the number of terms are three with common difference ’d’, then the three terms can be taken as a – d, a, a + d.
   ii. If the number of terms are four with common difference '2d', then the terms can be taken as a – 3d, a – d, a + d, a + 3d.
   iii. If the number of terms are five with common difference 'd', then the terms can be taken as a – 2d, a – d, a + d, a + 2d.
   iv. If the number of terms are six with common difference '2d', then the terms can be taken asa – 5d, a – 3d, a – d, a + d, a + 3d, a + 5d.
   v. If the terms of an A.P. are selected at regular intervals, then the selected terms form an A.P.
   Let a_n, a_n+1, a_n+2 be the consecutive terms of an A.P., then 2a_n+1 = a_n + a_n+2
   
   
5.  Properties of Arithmetic Progression
   • If a constant is added to each term of an A.P., the resulting sequence is also an A.P.
   • If a constant is subtracted from each term of an A.P., then the resulting sequence is also an A.P.
   • If each term of an A.P. is multiplied by a constant, then the resulting sequence is also an A.P.
   • If each term of an A.P. is divided by a non–zero constant, then the resulting sequence is also an A.P.
   
   
6. Geometric Progression
   • A sequence is said to be a geometric progression or G.P., if the ratio of any of its term to its preceding term is the same throughout. Constant ratio is common ratio denoted by ‘r’.
   
   • General term of a G.P.
   i. General form of a G.P. is a, ar, ar², ar³,... where ‘a’ is the first term and ‘r’ is the constant ratio, ‘r’ can take any non-zero real number.
   ii. General term of a G.P. is ar^n-1 where ‘a’ is the first term and r is the common ratio.
   • Sum of a G.P.
   i. Sum to first n terms of a G.P. is S_n = a + ar + ar² + … + ar^n-1
   ♦ If r = 1, S_n = a + a + a + … + a (n terms) = na
   ♦ If r < 1, S_n =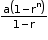 
   ♦ If r > 1, S_n = 
   ii. The sum of an infinite G.P. with first term ‘a’ and common ratio r ( –1 < r < 1) is given by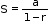 
   • Geometric Mean
   i. If three numbers are in G.P., then the middle term is called the geometric mean of the other two.
   ii. The geometric mean (G.M.) of any two positive numbers ‘a’ and ‘b’ is given by 
   iii. Let G₁, G₂,… G_n be n numbers between positive numbers a and b such that a, G₁, G₂, G₃,… G_n, b is a G.P.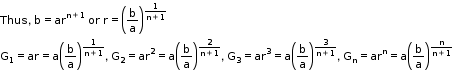
   
   
   • Selection of Terms
   i. If the number of terms of a G.P. is 3, with the common ratio r, then the selection of terms can be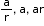 
   ii. If the number of terms of a G.P. is 4, with the common ratio  , then the selection of terms can be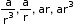 
   iii. If the number of terms of a G.P. is 5, with the common ratio r, then the selection of terms can be   
   
   
7. Properties of Geometric Progression
   • A sequence in geometric progression will remain in geometric progression if each of its terms is multiplied by a non-zero constant. 
   • A sequence obtained by multiplying two G.Ps term by term results in a G.P. with the common ratio is equal to the product of the common ratios of the two G.Ps.
   • The reciprocals of the terms of a given G.P. form a G.P. with common ratio .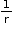
   • If each term of a G.P. be raised to the same power, the resulting sequence also forms a G.P.
   
   
8. Relation between A.M. and G.M.
   • If A and G be the A.M. and G.M. of two given positive real numbers ‘a’ and ‘b’ respectively, then
   A ≥ G where .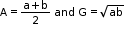
   Hence, the quadratic equation having a and b as its roots is x² – 2Ax + G² = 0
   • Let A and G be A.M. and G.M. of two given positive real numbers ‘a’ and ‘b’, respectively.
   Hence, the given numbers are: .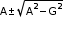
   • If A.M and G.M of two numbers are in the ratio of m : n, then the given numbers are in the ratio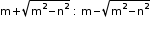 
   
   
9. Harmonic Progression
   • A sequence is said to be a harmonic progression or H.P., if the reciprocal of the numbers form an A.P.
   • General (n^th) term of an H.P.
   i. The n^th term of an H.P. is the reciprocal of the n^th term of the A.P. formed by the reciprocals of the terms of the H.P.
   ii. If the given H.P. is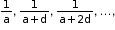  then its n^th term is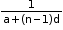  
   • Harmonic Mean
   i. If a, H, b are three quantities in H.P., then H is said to be the Harmonic Mean between a and b.
   ii. a, H, b are in H.P.  are in A.P.
   iii. If a₁, a₂, a₃, …, a_n are n non-zero numbers in H.P., then their harmonic mean will be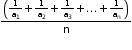 
   
   
10. Relation between A.P., G.P. and H.P.
    • Three numbers a, b, c will be in A.P., G.P. or H.P. according as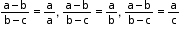 
    • If A, G and H are respectively the Arithmetic, Geometric and Harmonic Means between any two unequal positive numbers, then
    i. A, G, H are in G.P.
    ii. A > G > H
    
    
11. Arithmetico-Geometric Series
    • A series in which each term is the product of corresponding terms of an A.P. and a G.P. is called an Arithmetico-Geometric series.
    • General term of an Arithmetico-Geometric series
    i. The general or standard form of such a series is
    a + (a + d) + (a + 2d)r² + (a + 3d)r³ + … + {a + (n – 1)d}r^{n – 1}
    Here, each term if formed by multiplying the corresponding terms of the two series:
    A.P: a + (a + d) + (a + 2d) + … (a + (n – 1)d) + …
    G.P: 1 + r + r² + … + r^{n – 1} + …
    ii. N^th term of an Arithmetico-Geometric series is given by
    T_n = {a + (n – 1)d}r^{n – 1}
    
    • Sum of an Arithmetico-Geometric series
    i. The sum of the n terms of the series is given by
      
    ii. Sum of an infinite Arithmetico-Geometric series given by
      
    
    
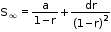
12. Special Series
    • The sum of  first ‘n’ natural numbers is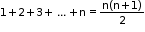
    
    • Sum of squares of the first n natural numbers is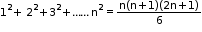
    
    • Sum of cubes of first n natural numbers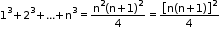
    
    • Sum of powers of 4 of first n natural numbers
     
    • Consider the series a₁ + a₂ + a₃ + a₄ + ... + a_n + ...
    If the differences a₂ - a₁, a₃ - a₂, a₄ - a₃, ... are in AP, then the n^th term is given by
    a_n = an² + bn + c, where a, b, c are constant.
    • Consider the series a₁ + a₂ + a₃ + a₄ + ... + a_n + ...
    If the differences a₂ - a₁, a₃ - a₂, a₄ - a₃, ... are in G.P., then the n^th term is given by
    a_n = ar^n-1 + bn + c, where a, b, c are constants.