Volume and Surface Area of Solids

Volume and Surface Area of Solids Synopsis

Synopsis

Surface area of a solid is the sum of the areas of all its faces.
The space occupied by a solid object is the volume of that object.
If l, b, h denote respectively the length, breadth and height of a cuboid, then:
Lateral surface area or Area of four walls = 2(ℓ + b) h
Total surface area = 2(ℓb + bh + hℓ)
Volume = ℓ x b x h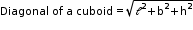
$begin mathsize 11px style Diagonal space of space straight a space cuboid equals square root of calligraphic l squared plus straight b squared plus straight h squared end root end style$
If the length of each edge of a cube is 'a' units, then:
Lateral surface area = 4 x (edge)²
Total surface area = 6 x (edge)²
Volume = (edge)³
$begin mathsize 11px style Diagonal space of space straight a space cube equals square root of 3 cross times space edge end style$
If r and h respectively denote the radius of the base and the height of a right circular cylinder, then:
Area of each end or Base area = πr²
Area of curved surface or lateral surface area = perimeter of the base x height = 2πrh
Total surface area (including both ends) = 2πrh + 2πr² = 2πr (h + r)
Volume = Area of the base x height = πr²h
If R and r respectively denote the external and internal radii of a right circular hollow cylinder and h denotes its height, then:
Area of each end = πR² - πr²
Area of curved surface = 2π(R + r)h
Total surface area = (Area of curved surface) + 2(Area of each end)
= 2π(R + r)h + 2 (πR²- πr²)
If r, h and l respectively denote the radius, height and slant height of a right circular cone, then:
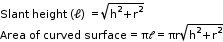
$begin mathsize 11px style Slant space height space left parenthesis straight ell right parenthesis space equals square root of straight h squared plus straight r squared end root Area space of space curved space surface equals straight pi calligraphic l equals πr square root of straight h squared plus straight r squared end root end style$
Total surface area = Area of curved surface + Area of base = πℓ + πr² = πr (ℓ + r)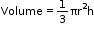
$begin mathsize 11px style Volume equals 1 third πr squared straight h end style$
If r is the radius of a sphere, then:
Surface area = 4πr²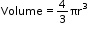
$begin mathsize 11px style Volume equals 4 over 3 πr cubed end style$
If r is the radius of a hemisphere, then:
Area of curved surface = 2πr²
Total surface Area = Area of curved surface + Area of base
= 2πr² + πr²
= 3πr²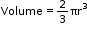
$begin mathsize 11px style Volume equals 2 over 3 πr cubed end style$
The total surface area of the solid formed by the combination of solids is the sum of the curved surface area of each of the individual solids.
The volume of the solid formed by the combination of basic solids is the sum of the volumes of each of the basic solids.
If a right circular cone is cut off by a plane parallel to its base, then the portion of the cone between the plane and the base of the cone is called a frustum of the cone.
If h is the height, l is the slant height, R and r are the radii of the upper and lower ends of a frustum of a cone, then:
Curved surface area = π (R + r) ℓ
Total surface area = π (R + r) ℓ + π[R² + r²]
$begin mathsize 11px style Volume equals 1 third πh open square brackets straight R squared plus straight r squared plus Rr close square brackets end style$
When a solid is melted and converted to another, volume of both the solids remains the same, assuming there is no wastage in the conversions. However, the surface area of the two solids may or may not be the same.
The solids having the same curved surface do not necessarily occupy the same volume and vice versa.