Plane Geometry: Circle

Synopsis

1. Introduction to Circle
   A circle is the locus of a point which lies in the plane in such a manner that its distance from a fixed point in the plane is constant. The fixed point is called the centre and the constant distance is called the radius of the circle.
   
   
2. Parts of the circle
   • A line segment that joins any two points lying on a circle is called the chord of the circle.
   • A chord passing through the centre of the circle is called diameter of the circle.
   • A line segment joining the centre and a point on the circle is called radius of the circle
   
   
   

• A line which intersects a circle at two distinct points is called a secant of the circle. In the below figure, AB is a secant to the circle.

1. Tangent to the circle
   A tangent to the circle is a line that intersects the circle (touches the circle) at only one point. The word ’tangent’ comes from the Latin word ‘tangere’, which means to touch. The common point of the circle and the tangent is called point of contact.
   
   
   In the figure, AB is a tangent to the circle and P is the point of contact.
   
   
2. Important facts about tangent
   • The tangent to a circle is a special case of the secant, when the two end points of its corresponding chord coincide.
   • The tangent at any point of a circle is perpendicular to the radius through the point of contact. This point of contact is also called as point of tangency.
   
   • A line drawn through the end of a radius (point on circumference) and perpendicular to it is a tangent to the circle. 
   
   
3. Number of tangents on a circle
   • There is no tangent possible to a circle from the point (or passing through a point) lying inside the circle.
   • There are exactly two tangents possible to a circle through a point outside the circle.
   • At any point on the circle, there can be one and only one tangent possible.
   
   
4. Length of the tangent
   The length of the segment of the tangent from the external point P and the point of contact with the circle is called the length of the tangent.
   • The lengths of tangents drawn from an external point to the circle are equal.
   • The figure shows two equal tangents (PA = PB) from an external point P.
   
5. Angle between two tangents from an external point
   • The centre of a circle lies on the bisector of the angle between the two tangents drawn from an external point.
   • Angle between two tangents drawn from an external point to a circle is supplementary to the angle formed by the line segment joining the points of contact to the centre.
   In the figure, angle P and angle Q are supplementary.
   
   
6. Perpendicular from the centre
   Perpendicular drawn from the centre to any chord of the circle, divides it into two equal parts.
   In the figure, OM is perpendicular to AB and AM = MB.
   
7. Normal to the circle
   The line containing the radius through the point of contact is called the normal to the circle at that point.
   
8. Inscribed circle
   Opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
   
   In the figure, angles 1 and 3 are supplementary. Accordingly, angles 2 and 4 are supplementary.
   
   
9. Common tangents
   • A common tangent is called a direct common tangent if both the circles lie on the same side of it.
   • The two direct common tangents are equal in length.
   • The length of a direct common tangent to two circles is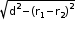 , where d is the distance between the centres of the circles and  are the radii of the circles.
   • A common tangent is called transverse common tangent if the circles lie on opposite sides of it.
   In this figure AB and CD are two transverse common tangent.
   The two transverse common tangents are equal in length.
   
   
10. Segment of a chord and its properties
    • If two chords of a circle intersect internally or externally, then the products of the lengths of segments are equal.
    PA × PB = PC × PD
    • If two line segments AB and CD intersect at P or lines containing segments AB and CD intersect at P such that PA × PB = PC × PD, then the four points A, B, C and D are concyclic.
    • If a line touches a circle and from the point of contact a chord is drawn, the angles between the tangent and the chord are respectively equal to the angles in the corresponding alternate segment.
    • If a line is drawn through an end of a chord of a circle so that the angle formed with the chord is equal to the angle subtended by the chord in the alternate segment, then the line is a tangent to the circle.
    • If a chord (AB) and a tangent (PT) intersect externally (at P) then the product of the lengths of the end points of the chord from P, is equal to the square of the length of the tangent from the point of contact to the point of intersection, that is PA × PB = PT²