Probability
Probability Synopsis
Synopsis
- A random experiment is an experiment which produces a set of well-defined possible outcomes under identical conditions.
- Elementary event: Each outcome of the random experiment is called an elementary event.
- Sample space: The set of all possible outcomes of the random experiment is called the sample space.
- Event: In a random experiment, the subset of the sample space is called an event.
- Certain event (sure event): If a random experiment occurs always, then the corresponding event is called a certain event.
- Impossible event: If a random experiment never occurs, then the corresponding event is called an impossible event.
- Mutually exclusive event: In a random experiment, if the occurrence of any one of the event prevents the occurrence of all the other events, then the corresponding events are said to be mutually exclusive.
- Exhaustive event: In a random experiment, if the union of two or more events forms the sample space, then the associated events are said to be exhaustive events.
- Probability of an event: In a random experiment of n elementary events, if m events are favourable to an event A, then the probability of occurrence of A is denoted by P(A) and P(A) =
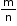 .
. - Probability of a sure event is 1 and probability of an impossible event is 0.
- Addition theorem: In a random experiment, if A and B are two associated events, then
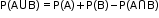
- If A and B are two mutually exclusive events, then
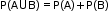
- In a random experiment, if A, B and C are three associated events, then
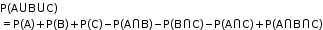
- If A, B and C are three mutually exclusive events, then
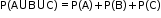
- If A and B are two events, then the probability of occurrence of A only is

- If A and B are two events, then the probability of occurrence of B only is
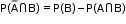
- If A and B are two events, then the probability of occurrence of exactly one of A and B is 18.
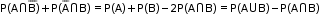
- The probability that event B will occur, given the knowledge that event A has already occurred, is called conditional probability. It is denoted as P(B|A).
- Conditional probability of B given A has occurred P(B|A) is given by the ratio of the number of events favourable to both A and B to the number of events favourable to A.
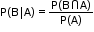
- If E and F are two events associated with sample space S, then 0 ≤ P (E/F) ≤ 1.
- If E and F are the events of a sample space S of an experiment, then
i. P(S|F) = P(F|F) = 1
ii. For any two events A and B of sample space S, if F is another event such that P(F) ≠ 0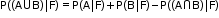
iii. P(E’|F) = 1 − P(E|F) - Multiplication rule of probability for more than two dependent events, If A, B and C are three events of sample space, we have

- Two events A and B are independent if and only if the occurrence of A does not depend on the occurrence of B and vice versa.
- If events A and B are independent, then P(B|A) = P(B) and P(A|B) = P(A).
- Three events A, B and C are independent if they are pairwise independent i.e.
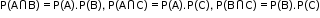
- Three events A, B and C are independent if
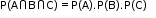
Independence implies pairwise independence, but not conversely. - Bayes' theorem is also known as the formula for the probability of ‘causes’.
- If E1, E2, ... En are n non-empty events which constitute a partition of sample space S and A is any event of non-zero probability, then by Bayes’ theorem

Top Formulae
- 0 ≤ P(B|A) ≤ 1
- If E and F are two events associated with the same sample space of a random experiment, then the conditional probability of the event E given that F has occurred, i.e. P(E|F) is given by
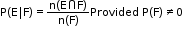
- Multiplication theorem
a. For two events:
If E and F are two events associated with a sample space S, then = P(E) P(F|E) = P(F) P(E|F) provided P(E) ≠ 0 and
= P(E) P(F|E) = P(F) P(E|F) provided P(E) ≠ 0 and
P(F) ≠ 0.
b. For three events:
If E, F and G are three events of sample space S, then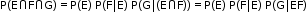
- Multiplication theorem for independent events
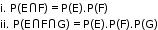
- Let E and F be two events associated with the same random experiment. The two events E and F are said to be independent if
i. P(F|E) = P(F) provided P(E) ≠ 0 and
ii. P(E|F) = P(E) provided P(F) ≠ 0
iii. = P(E).P(F)
= P(E).P(F) - Theorem of total probability
Let {E1, E2,...,En} be a partition of the sample space S, and suppose that each of the events E1, E2, ... En has non-zero probability of occurrence. Let A be any event associated with S, then
P(A) = P(E1) P(A|E1) + P(E2) P(A|E2) + ... + P(En) P(A|En)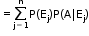
Download complete content for FREE 

