Trigonometric Equations

Synopsis

1. If a point on a unit circle is on the terminal side of an angle in the standard position, then the sine of such an angle is simply the y-coordinate of the point and the cosine of the angle is the x-coordinate of that point.
   
   
2. All the angles which are integral multiples of 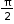 are called quadrantal angles. Values of quadrantal angles are:
    
   
   
3. Trigonometric functions as even or odd
   • A function f(x) is said to be an even function if f(-x) = f(x), for all x in its domain.
   • A function f(x) is said to be an odd function if f(-x) = -f(x), for all x in its domain.
   • Cosine is an even function and sine is an odd function since cos(−x) = cos x and sin(−x) = −sin x
   
   
4. Sign of trigonometric functions in various quadrants
   • In quadrant I, all the trigonometric functions are positive.
   • In quadrant II, only sine and cosec functions are positive.
   • In quadrant III, only tan and cot functions are positive.
   • In quadrant IV, only cosine and sec functions are positive.
   • This is depicted as follows:
   
   • In quadrants, where the y-axis is positive (i.e. I and II), sine is positive, and in quadrants where the x-axis is positive (i.e. I and IV), cosine is positive.
   • A simple rule to remember the sign of the trigonometrical ratios, in all the four quadrants, is the four letter phrase—All Silver Tea Cups.
   
   
5. Period of a function
   A function ‘f’ is said to be a periodic function if there exists a real number T > 0 such that f(x + T) = f(x) for all ‘x’. This ‘T’ is the period of function.
   
   
6. Trigonometric ratios of complementary angles
   i. sin (90° - θ) = cos θ
   ii. cos (90° - θ) = sin θ
   iii. tan (90° - θ) = cot θ
   iv. cosec (90° - θ) = sec θ
   v. sec (90° - θ) = cosec θ
   vi. cot (90° - θ) = tan θ
   
   
7. Trigonometric ratios of (90° + θ) in terms of θ
   i. sin (90° + θ) = cos θ
   ii. cos (90° + θ) = -sin θ
   iii. tan (90° + θ) = -cot θ
   iv. cosec (90° + θ) = sec θ
   v. sec (90° + θ) = -cosec θ
   vi. cot (90° + θ) = -tan θ
   
   
8. Trigonometric ratios of (180° - θ) in terms of θ
   i. sin (180° - θ) = sin θ
   ii. cos (180° - θ) = -cos θ
   iii. tan (180° - θ) = -tan θ
   iv. cosec (180° - θ) = cosec θ
   v. sec (180° - θ) = -sec θ
   vi. cot (180° - θ) = -cot θ
   
   
9. Trigonometric ratios of (180° + θ ) in terms of θ
   i. sin (180° + θ) = -sin θ
   ii. cos (180° + θ) = -cos θ
   iii. tan (180° + θ) = tan θ
   iv. cosec (180° + θ) = -cosec θ
   v. sec (180° + θ) = -sec θ
   vi. cot (180° + θ) = cot θ
   
   
10. Trigonometric ratios of (360° - θ ) in terms of θ
    i. sin (360° - θ) = -sin θ
    ii. cos (360° - θ) = cos θ
    iii. tan (360° - θ) = -tan θ
    iv. cosec (360° - θ) = -cosec θ
    v. sec (360° - θ) = sec θ
    vi. cot (360° - θ) = -cot θ
    
    
11. Trigonometric ratios of (360° + θ ) in terms of θ
    i. sin (360° + θ) = sin θ
    ii. cos (360° + θ) = cos θ
    iii. tan (360° + θ) = tan θ
    iv. cosec (360° + θ) = cosec θ
    v. sec (360° + θ) = sec θ
    vi. cot (360° + θ) = cot θ
    
    
12. General and particular solutions
    • The solutions of a trigonometric equation, for which 0 ≤ x ≤ 2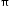, are called principal solutions.
    • The expression involving the integer ‘n’, which gives all the solutions of a trigonometric equation, is called the general solution.
    
    
13. Principal value
    • The numerically smallest value of the angle (in degree or radian) satisfying a given trigonometric equation is called the Principal Value.
    • If there are two values, one positive and the other negative, which are numerically equal, then the positive value is taken as the Principal Value.
    
    
14. Trigonometric equations
    
    
    
15. Sine Rule: The sine rule states that
    
    
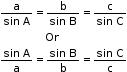
16. Laws of Cosine
    
    
    
    
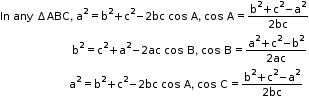
17. Domain and range of various trigonometric functions
    
    
    
18. Graphs of trigonometric functions
    Graphs help in the visualization of the properties of trigonometric functions.
    The graph of y = sinθ can be drawn by plotting a number of points (θ, sinθ) as θ takes a series of different values.
    i. Graph of sin x
    
    ii. Graph of cos x
    
    iii. Graph of tan x
    
    iv. Graph of sec x
    
    v. Graph of cosec x
    
    vi. Graph of cot x