Heights and Distances

Synopsis

1. Trigonometric Ratios
   Ratio of the sides of a right triangle with respect to the acute angles is called the trigonometric ratios of the angle.
   Trigonometric ratios of acute angle A in right triangle ABC are given below:
   
   The values of the trigonometric ratios of an angle do not vary with the length of the sides of the triangle, if the angles remain the same.
   
   
2. Relation between trigonometric ratios
   The ratios cosec A, sec A and cot A are the reciprocals of the ratios sin A, cos A and tan A respectively as given: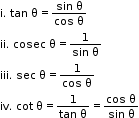
   
   
   
   
3. Values of Trigonometric ratios of some specific angles:
   
   
   
4. Trigonometric ratios of complementary angles
   Two angles are said to complementary angles if their sum is equal to 90°. Based on this relation, the trigonometric ratios of complementary angles are given as follows:
   i. sin (90° – A) = cos A
   ii. cos (90° – A) = sin A
   iii. tan (90° – A) = cot A
   iv. cot (90° – A) = tan A
   v. sec (90° – A) = cosec A
   vi. cosec (90° – A) = sec A
   Note: tan 0° = 0 = cot 90°, sec 0° = 1 = cosec 90°, sec 90°, cosec 0°, tan 90° and cot 0° are not defined.
   
   
5. Basic trigonometric identities:
   i. sin² θ + cos² θ = 1
   ii. 1 + tan² θ = sec² θ
   iii. 1 + cot² θ = sec² θ
   
   
6. The height or length of an object or the distance between two distant objects can be determined by the help of trigonometric ratios.
    
7. Line of sight
   The line of sight is the line drawn from the eye of an observer to the point in the object viewed by the observer.
   
   
8. Angles of elevation and depression
   • The angle of elevation of an object viewed is the angle formed by the line of sight with the horizontal when it is above the horizontal level, i.e., the case when we raise our head to look at the object.
   
   • The angle of depression of an object viewed is the angle formed by the line of sight with the horizontal when it is below the horizontal level, i.e., the case when we lower our head to look at the object.
   
9. Pythagoras theorem
   It states that “In a right triangle, square of the hypotenuse is equal to the sum of the square of the other two sides”.
   • When any two sides of a right triangle are given, its third side can be obtained by using Pythagoras theorem.
   
   
10. Reflection from the water surface
    In case of reflection from the water surface, the two heights above and below the ground level are equal in length.