Mathematical Induction
Mathematical Induction Synopsis
Synopsis
Top Concepts
- There are two types of reasoning — deductive and inductive.
- In deduction, given a statement to be proven, often called a conjecture or a theorem, valid deductive steps are derived and a proof may or may not be established.
- Deduction is the application of a general case to a particular case.
- Inductive reasoning depends on working with each case and developing a conjecture by observing the incidence till each and every case is observed.
- ‘Induction’ means the generalization from particular cases or facts.
- Deductive approach is known as the ‘top-down approach’. The given theorem is narrowed down to a specific hypothesis then to observation. Finally the hypothesis is tested with specific data to get the confirmation (or not) of the original theory.
- Inductive reasoning works the other way, moving from specific observations to broader generalizations and theories. Informally, this is known as the ‘bottom up approach’.
- To prove statements or results formulated in terms of n, where n is a positive integer, a principle based on inductive reasoning called the Principle of Mathematical Induction is used.
- The Principle of Mathematical Induction or PMI is one such tool which can be used to prove a wide variety of mathematical statements. Each such statement is assumed as P (n) associated with positive integer n, for which the correctness for the case n = 1 is examined. Then assuming the truth of P(k) for some positive integer k, the truth of P (k + 1) is established.
- Let p(n) denote a mathematical statement such that
• p(1) is true i.e. the statement is true for n = 1.
• p(k + 1) is true whenever p(k) is true i.e. if the statement is true for n = k, then the statement is also true for n = k + 1.
Then the statement is true for all natural numbers ‘n’ by the Principle of Mathematical Induction. - PMI is based on Peano’s Axiom.
- PMI is based on a series of well-defined steps so it is necessary to verify all of them.
- PMI can be used to prove the equality, inequality and divisibility of natural numbers.
Key Formulae
- Sum of n natural numbers: 1 + 2 + 3 +….+ n =

- Sum of n2 natural numbers: 12 + 22 + 32 +………n2 =
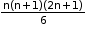
- Sum of odd natural numbers: 1 + 3 + 5 + 7……+ (2n - 1) = n2
- Steps of PMI
• Denote the given statement in terms of ‘n’ by P(n).
• Check whether the proposition is true for n = 1.
• Assume that the proposition result is true for n = k.
• Using p(k), prove that the proposition is true for p(k + 1). - Rules of Inequalities
• If a < b and b < c then a < c.
• If a < b then a + c < b + c.
• If a < b and c > 0 which means c is positive, then ac < bc.
• If a < b and c < 0 which means c is negative, then ac > bc.
Download complete content for FREE 

