Binomial Theorem

Synopsis

1. Introduction to Binomial Expansion
   • A binomial expression is an algebraic expression having two terms. For example, (a + b), (a - b) etc.
   • The expansion of a binomial for any positive integral exponent ‘n’ is given by the binomial theorem. The binomial theorem says that
   (x + y)ⁿ = xⁿ + ⁿC₁x^n-1y + ⁿC₂x^n-2y² + ---- + ⁿC_rx^n-ry^r + ----- + ⁿC_n-1xy^n-1 + ⁿC_nyⁿ
   • In summation notation,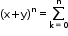  ⁿC_kx^n-ky^k
   
   
2. Properties of Binomial Expansion
   • In the binomial expansion of (x + y)ⁿ the number of terms is (n + 1) i.e. one more than the exponent.
   • The exponent of ‘x’ goes on decreasing by unity and that of ‘y’ increases by unity. Exponent of ‘x’ is ‘n’ in the first term, (n - 1) in the second term, and so on ending with zero in the last term.
   • The sum of the indices of ‘x’ and ‘y’ is always equal to the index of the expression.
   • Replacing a by –a in the expansion of (x + y)ⁿ, we have
   (x – y)ⁿ = [x + (-y)]ⁿ
   (x – y)^ⁿ = ⁿC₀xⁿ - ⁿC₁x^n-1y + ⁿC₂x^n-2y² - ⁿC₃x^n-3y³ + … + (-1)^{n n}C_nyⁿ
   In summation notation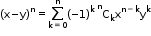  
   • (x + y)ⁿ + (x - y)ⁿ = 2[ⁿC₀xⁿy⁰ + ⁿC₂x^n-2y² + ⁿC₄x^n-4y⁴ + ...]
   and
   (x + y)ⁿ - (x - y)ⁿ = 2[ⁿC₁x^n-1y¹ + ⁿC₃x^n-3y³ + ⁿC₅x^n-5y⁵ + ...]
   • If n is odd, then {(x + y)ⁿ + (x - y)ⁿ} and {(x + y)ⁿ - (x - y)ⁿ} both have the same number of terms equal to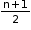 
   • If n is even, then {(x + y)ⁿ + (x - y)ⁿ}  has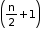  terms and {(x + y)ⁿ - (x - y)ⁿ} has  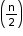terms.
3. General and Middle Terms
   • General Term
   i. General term in the expansion of (x + y)ⁿ is T_k+1 = ⁿC_kx^n-ky^k
   ii. General term in the expansion of (x - y)ⁿ is T_k+1 = ⁿC_k(-1)^kx^n-ky^k
   • Term from the end
   In the binomial expansion of (x + y)ⁿ, the k^th term from the end is ((n + 1) - k + 1) = (n - k + 2)^th term from the beginning.
   • Middle Term(s)
   i. If n is even, there is only one middle term in the expansion of (x + y)ⁿ and it will be the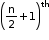  term.
   ii. If n is odd, there are two middle terms in the expansion of (x + y)ⁿ, i.e. the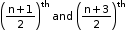  term.
   iii. In the expansion of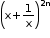  , where x ≠ 0, the middle term is  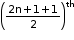i.e., (n + 1)^th term, as 2n is even.
   
   
4. Binomial Coefficients
   • The coefficients, the number of combinations of n objects taken r at a time, occurring in the binomial expansion, are known as binomial coefficients.
   • The coefficients ⁿC_r of terms equidistant from the beginning and end are equal. These coefficients are known as binomial coefficients.
   i.e. ⁿC_r = ⁿC_n-r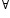  r = 0, 1, 2, ..., n
   • Coefficient of (k + 1)^th term in the binomial expansion of (1 + x)ⁿ is ⁿC_k.
   • Coefficient of X^k term in the binomial expansion of (1 + x)ⁿ is ⁿC_k.
   • Coefficient of X^k term in the binomial expansion of (1 - x)ⁿ is (-1)^k nC_k.
   • Coefficient of (k + 1)^th term in the binomial expansion of (1 - x)ⁿ is (-1)^k nC_k.
   
   
5. Binomial theorem for negative or fractional index
   • Let n be a negative integer or a fraction (+ve or –ve) and x be a real number such that | x | < 1, then
   
   • General Term
   General term in the expansion of (1 + x)ⁿ  when n is negative or fractional is given by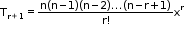
   
   
   
6. Some special expansions
   • (1 - x)^-1 = 1 + x + x² + ... + x^r + ...
   • (1 + x)^-1 = 1 - x + x² - ... + (-1)^rx^r + ...