Matrices and Determinants

Synopsis

1. Matrix and its elements
   • A matrix is an ordered rectangular array of numbers (real or complex) or functions or names or any type of data. The numbers or functions are called the elements or the entries of the matrix.
   • The horizontal lines of elements constitute the rows of the matrix and the vertical lines of elements constitute the columns of the matrix.
   • Each number or entity in a matrix is called its element.
   
   
2. Order of a Matrix
   • If a matrix contains m rows and n columns, then it is said to be a matrix of the order m × n (read as m by n).
   • The total number of elements in a matrix is equal to the product of its number of rows and number of columns.
   
   
3. Row and Column matrix
   • A matrix is said to be a column matrix if it has only one column.
   • A = [a_ij]_{m x 1} is a column matrix of order m × 1.
   • A matrix is said to be a row matrix if it has only one row.
   • B = [b_ij]_{1 x n} is a row matrix of order 1 × n.
   
   
4. Rectangular Matrix and Zero Matrix
   • A matrix in which the number of rows is not equal to the number of columns is called a rectangular matrix.
   • A matrix each of whose all elements are zero is called a zero matrix or null matrix.
   
   
5. Square Matrix and Types of Square Matrices
   • A matrix in which the number of rows is equal to the number of columns is said to be a square matrix. A matrix of order ‘m × n’ is said to be a square matrix if m = n and is known as a square matrix of order ‘n’.
   • A square matrix which has every non–diagonal element as zero is called a diagonal matrix.
   • A square matrix A = [a_ij]_{m x m} is said to be a diagonal matrix if all its non-diagonal elements are zero, i.e. a matrix A = [a_ij]_{m x m} is said to be a diagonal matrix if a_ij = 0 when i ≠ j.
   • A square matrix in which the elements in the diagonal are all 1 and the rest are all zero is called an identity matrix. A square matrix A = [a_ij]_{n x n} is an identity matrix if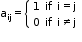 
   • A diagonal matrix is said to be a scalar matrix if its diagonal elements are equal, that is a square matrix B = [b_ij]_{n x n} is said to be a scalar matrix if b_ij = 0 when i ≠ j and bij = k when i = j for some constant k.
   
   
6. Sub-matrix
   A matrix obtained by deleting the rows or columns or both of a matrix is called a sub-matrix.
   
   
7. Upper triangular matrix
   A square matrix A = [a_ij] is called an upper triangular matrix if a_ij = 0 for all i > j. In an upper triangular matrix, all elements below the main diagonal are zero.
   
   
8. Lower triangular matrix
   A square matrix A = [a_ij] is called a lower triangular matrix if a_ij = 0 for all i < j. In a lower triangular matrix, all elements above the main diagonal are zero.
   
   
9. Equality of Matrices
   • Two matrices are said to be equal if they are of the same order and have the same corresponding elements.
   • Two matrices A = [a_ij] and B = [b_ij] are said to be equal if they are of the same order. Each element of A is equal to the corresponding element of B, i.e., a_ij = b_ij for all i and j.
   
   
10. Transpose of a Matrix
    • If A is a matrix, then its transpose is obtained by interchanging its rows and columns.
    • In other words, if A = [a_ij] be an m × n matrix, then the matrix obtained by interchanging the rows and columns of A is called the transpose of A.
    • Transpose of the matrix A is denoted by A’ or (A^T). That is, (A^T)_ij = a_ji for all i = 1, 2, … m; j = 1, 2, … n.
    
    
11. Properties of transpose of matrices
    • If A is a matrix, then (A^T )^T = A
    • (A + B)^T = A^T + B^T
    • (kB)^T = kB^T, where k is any constant.
    • If A and B are two matrices such that AB exists, then (AB)^T = B^T A^T. 
    • If A, B and C are three matrices such that ABC exists, then (ABC)^T = C^T B^T A^T.
    
    
12. Symmetric and Skew-symmetric Matrix
    • If A = [a_ij]_{n × n} is an n × n matrix such that A^T = A, then A is called a symmetric matrix.
    • In a symmetric matrix, a_ij = a_ji for all i and j.
    • If A = [a_ij]_{n × n} is an n × n matrix such that A^T = –A, then A is called a skew-symmetric matrix.
    • In a skew-symmetric matrix, a_ij = -a_ji.
    • All main diagonal elements of a skew-symmetric matrix are zero.
    • Every square matrix can be expressed as the sum of a symmetric and a skew-symmetric matrix.
    • All positive integral powers of a symmetric matrix are symmetric.
    • All odd positive integral powers of a skew-symmetric matrix are skew-symmetric. 
    
    
13. Properties of Symmetric and Skew-symmetric matrices
    • The sum of two symmetric matrices is a symmetric matrix.
    • Every square matrix can be expressed as the sum of a symmetric and a skew-symmetric matrix, i.e.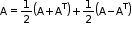  for any square matrix A.
    • The sum of two skew symmetric matrices is a skew symmetric matrix.
    • For a symmetric matrix A and a scalar k, kA is a symmetric matrix.
    • For a skew-symmetric matrix A and a scalar k, kA is a skew-symmetric matrix.
    • If A be any square matrix, then A + A′ is symmetric and A – A′ is skew symmetric.
    
    
14. Addition of Matrices
    • If A = [a_ij]_{m × n} and B = [b_ij]_{m × n} are two matrices of the order m × n, then their sum is defined as a matrix C = [c_ij]_{m × n} where c_ij = a_ij + b_ij for 1 ≤ i ≤ m, 1 ≤ j ≤ n.
    • Two matrices can be added (or subtracted) if they are of the same order.
    
    
15. Multiplication of a Matrix by a Scalar
    • For multiplying two matrices A and B, the number of columns in A must be equal to the number of rows in B.
    • If A = [a_ij]_{m × n} is a matrix and k is a scalar, then kA is another matrix which is obtained by multiplying each element of A by the scalar k.
    • Hence, kA = [ka_ij]_{m × n}
    
    
16. Difference of Matrices
    If A = [a_ij]_{m × n} and B = [b_ij]_m×n two matrices, then their difference is represented a A - B = A + (-1)B
    
    
17. Properties of matrix addition
    • Matrix addition is commutative, i.e. A + B = B + A
    • Matrix addition is associative, i.e. (A + B) + C = A + (B + C)
    • Existence of additive identity
    Null matrix is the identity with respect to addition of matrices.
    Given a matrix A = [a_ij]_{m × n}, there will be a corresponding null matrix O of the same order such that A + O = O + A = A
    • Existence of additive inverse
    Let A = [a_ij]_{m × n} be any matrix, then there exists another matrix –A = −[a_ij]_{m × n} such that A + (–A) = (–A) + A = O.
    
    
18. Cancellation law
    If A, B and C are three matrices of the same order, then
    A + B = A + C ⇒ B = C and
    B + A = C + A ⇒ B = C
    
    
19. Properties of scalar multiplication of matrices
    If A = [a_ij], B = [b_ij] are two matrices, and k and L are real numbers, then
    • k(A + B) = kA + kB
    • (k + L)A = kA + LA
    • k(A + B) = k([a_ij]+[b_ij]) = k[a_ij] + k[b_ij] = kA + kB
    • (k + L)A = (k + L)[a_ij] = [(k + L)aij] + k[a_ij] + L[a_ij] = kA + LA
    
    
20. Multiplication of two Matrices
    If A = [a_ij]_{m × p}, B = [b_ij]_{p × n} are two matrices, then their product AB is given by C = [c_ij]_{m × n} such that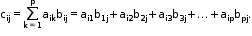
    
    The product of two matrices A and B is defined if the number of columns in A = the number of rows in B. 
    
    
21. Properties of Matrix Multiplication
    • Commutative law does not hold in matrices. In general, AB ≠ BA.
    • Matrix multiplication is associative i.e. for any three matrices A, B and C, A(BC) = (AB)C.
    • Distributive law: For any three matrices A, B and C
    i. A(B + C) = AB + AC
    ii. (A + B)C = AC + BC
    • The multiplication of two non-zero matrices can result in a null matrix.
    • Existence of Multiplicative Identity
    For every square matrix A, there exist an identity matrix of the same order such that |A = A| = A
    
    
22. If A is a square matrix, then we define A¹ = A and Aⁿ⁺¹ = Aⁿ.A
    
    
23. If A is a square matrix, a₀, a₁, a₂, ..., a_n are constants, then
    a₀Aⁿ + a₁A^n-1 + a₂A^n-2 + ... + a_n-1A + a_n is called a matrix polynomial.
    
    
24. If A, B and C are matrices, then AB = AC, A ≠ 0 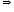B = C.
    In general, the cancellation law is not applicable in matrix multiplication.
    
    
25. Elementary Operations
    There are six elementary operations on matrices—three on rows and three on columns.
    • Interchanging the two rows, i.e. R_i ↔ R_j implies that the i^th row is interchanged with the j^th row.
    The two rows are interchanged with one another and the rest of the matrix remains the same.
    • Multiplying a row with a scalar or a real number, i.e. R_i → kR_i that i^th row of a matrix A is multiplied by k.
    • The addition to the elements of any row, the corresponding elements of any other row multiplied by any non-zero number, i.e. R_i → R_i +kR_j k multiples of the j^th row elements are added to the i^th row elements.
    • Interchanging the two columns: C_r ↔ C_k indicates that the r^th column is interchanged with the k^th column.
    • Multiplying a column with a non-zero constant, i.e. C_i → kC_i
    • The addition of a scalar multiple of any column to another column, i.e. C_i → C_i + kC_i
    • Elementary operations help in transforming a square matrix to an identity matrix.
    • Either of the two operations—row or column—can be applied. Both cannot be applied simultaneously.
    
    
26. Inverse of a Matrix by Elementary Operations
    • The inverse of a square matrix, if it exists, is unique. 
    • The inverse of a matrix can be obtained by applying elementary row or column operations on the matrix A.
    • In order to find A^-1 using row operation, write A = lA and apply a sequence of row operations till we get l = BA, where B is the inverse of A.
    • In order to find A^-1 using column operation, write A = Al and apply a sequence of column operations till we get l = AB, where B is the inverse of A.
    
    
27. Introduction to Determinant of a Matrix
    • To every square matrix A = [a_ij], a unique number (real or complex) called the determinant of the square matrix A can be associated.
    • The determinant of matrix A is denoted by det(A) or |A| or Δ.
    • Only square matrices can have determinants.
    • A determinant can be thought of as a function which associates each square matrix to a unique number (real or complex).
    • f : M → K is defined by f(A) = k, where A ε M set of square matrices and k ε K set of numbers (real or complex).
    
    
28. Determinant of a Matrix of order one
    Let A = [a] be a matrix of order 1, then the determinant of A is defined to be equal to a.
    
    
29. Determinant of a Matrix of order 2 × 2
    
    
    
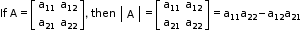
30. Determinant of a Matrix of order 3 × 3
    
    
    
    
31. Calculation of Determinant
    A determinant can be expanded along any of its rows (or columns). For easier calculations, it must be expanded along the row (or column) containing maximum zeroes.
    
    
32. Value of the Determinant
    • The value of determinant of a matrix A is obtained by the sum of the product of the elements of a row (or column) with its corresponding cofactors.
    Example: |A| = a₁₁A₁₁ + a₁₂A₁₂ + a₁₃A₁₃
    • If elements of a row (or column) are multiplied with cofactors of any other row (or column), then their sum is zero.
    Example: a₁₁A₂₁ + a₁₂A₂₂ + a₁₃A₂₃ = 0
    
    
33. Minor of an Element
    • Minor of an element a_ij of a determinant is the determinant obtained by deleting its i^th row and j^th column in which the element a_ij lies.
    • Minor of an element a_ij is denoted by M_ij.
    • The minor of an element of a determinant of order n(n ≥ 2) is a determinant of order n – 1.
    
    
34. Co-factor and Adjoint
    • Cofactor of an element a_ij, denoted by A_ij is defined by A_ij = (−1)^i+j.M_ij, where M_ij is the minor of a_ij.
    • The adjoint of a square matrix A = [a_ij] is the transpose of the cofactor matrix [A_ij]n × n.
    
    
35. Singular and Non-singular Matrices
    • A square matrix A is said to be singular if |A| = 0.
    • A square matrix A is said to be non-singular if |A| ≠ 0.
    • If A and B are non-singular matrices of the same order, then AB and BA are also non-singular matrices of the same order.
    
    
36. Determinant of product of Matrices
    The determinant of the product of two matrices is equal to the product of the respective determinants, i.e. |AB| = |A||B|, where A and B are square matrices of the same order.
    
    
37. Consistent or Inconsistent System of Equations
    • A system of equations is said to be consistent if its solution (one or more) exists.
    • A system of equations is said to be inconsistent if its solution does not exist.
    
    
38. Properties of Determinants
    • Property 1
    Value of the determinant remains unchanged if its rows and columns are interchanged. If A is a square matrix, then det(A) = det(A’), where A’ = transpose of A.
    
    • Property 2
    If any two rows (columns) of a determinant are interchanged, then the value of the determinant changes by a minus sign only.
    
    • Property 3
    If any two rows (or columns) of a determinant are identical, then the value of the determinant is zero.
    
    • Property 4
    If A = [a_ij] is a square matrix of order n and B is the matrix obtained from A by multiplying each element of a row (or column) of A by a constant k, then its value gets multiplied by k.
    If Δ₁ is the determinant obtained by applying R_i → kR_i or C_i → kC_i to the determinant Δ, then Δ₁ = kΔ. Thus, |B| = k|A|. This property enables removing the common factors from a given row or column.
    If A is a square matrix of order n and k is a scalar, then |kA| = kⁿ |A|.
    
    • Property 5
    If in a determinant, the elements in two rows or columns are proportional, then the value of the determinant is zero.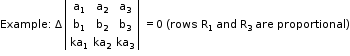
    
    
    • Property 6
    If the elements of a row (or column) of a determinant are expressed as the sum of two terms, then the determinant can be expressed as the sum of the two determinants.
    
    • Property 7
    If to any row or column of a determinant, a multiple of another row or column is added, then the value of the determinant remains the same, i.e. the value of the determinant remains the same on applying the operation R_i → R_i + kRj  or C_i → C_i + kC_j.
    
    • Property 8
    Let A be a square matrix of order n(≥ 2) such that each element in a row (or column) of A is zero, then |A| = 0.
    
    • Property 9
    If A = [a_ij] is a diagonal matrix of order n(≥ 2), then |A| = a₁₁. a₂₂. a₃₃. .... . a_nn   
    
    • Property 10
    If A and B are square matrices of the same order, then |AB| = |A|.|B|
    
    • Property 11
    If more than one operation such as R_i → R_i + kR_j is done in one step, care should be taken to see that a row which is affected in one operation should not be used in another operation. A similar remark applies to column operations.
    
    
39. Determinant of a Skew-symmetric Matrix
    • If A is a skew-symmetric matrix of odd order, then |A| = 0.
    • The determinant of a skew symmetric matrix of even order is a perfect square.
    
    
40. Adjoint of a matrix
    • The adjoint of a square matrix A = [a_ij]_{n × n} is defined as the transpose of the matrix [A_ij]_{n × n}, where A_ij is the cofactor of the element a_ij.
    • Adjoint of the matrix A is denoted by adj A.
    • If A is any given square matrix of order n, then A (adj A) = (adj A) A = |A| l, where l is the identity matrix of order n.
    • If A and B are two non-singular matrices of the same order, then adj (AB) = (adj B) (adj A).
    
    
41. Inverse of a Matrix
    • Let A and B be two square matrices of the order n such that AB = BA = l. Then A is called the inverse of B and is denoted by B = A⁻¹.
    • If B is the inverse of A, then A is also the inverse of B.
    • A square matrix A is invertible, i.e. its inverse exists if and only if A is a non-singular matrix.
    Inverse of matrix A (if it exists) is given by .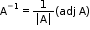
    • If A and B are two invertible matrices of the same order, then (AB)⁻¹ = B⁻¹ A⁻¹.
    
    
42. Properties of a Non-singular Matrix
    • A square matrix is invertible if and only if A is a non-singular matrix.
    • The adjoint of a symmetric matrix is also a symmetric matrix.
    • If A is a non-singular matrix of order n, then |adj.A| = |A|ⁿ⁻¹.
    • If A and B are non-singular matrices of the same order, then AB and BA are also non-singular matrices of the same order.
    • If A is a non-singular square matrix, then adj (adj A) = |A|ⁿ⁻²A.
    
    
43. Solution of System of Linear Equations
    • Determinants and matrices can also be used to solve the system of linear equations in two or three variables.
    • System of linear equations
    a₁x + b₁y + c₁z = d₁
    a₂x + b₂y + c₂z = d₂
    a₃x + b₃y + c₃z = d₃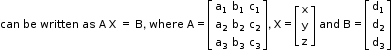  
    
    • Then matrix X = A⁻¹B gives the unique solution of the system of equations if |A| is non-zero and A⁻¹ exists.
    
    
44. Conditions of consistency and inconsistency of linear equations
    • For a system of two simultaneous linear equations with two unknowns
    i. If D ≠ 0, then the given system of equations is consistent and has a unique solution, given by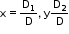 
    ii. If D = 0 and D₁ = D₂ = 0, then the system is consistent and has infinitely many solutions.
    iii. If D = 0 and one of D₁ and D₂ is non-zero, then the system is inconsistent.
    • For a system of three simultaneous linear equations with three unknowns
    i. If D ≠ 0 , then the given system of equations is consistent and has a unique solution given by .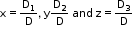
    ii. If D = 0 and D₁ = D₂ = D₃ = 0, then the system is consistent and has infinitely many solutions.
    
    
45. Area of a Triangle
    • Because area is a positive quantity, the absolute value of the determinant is taken in case of finding the area of a triangle.
    • If the area is given, then both positive and negative values of the determinant are used for calculation.
    • The area of a triangle formed by three collinear points is zero.
    
    
46. Some Special Matrices
    • Nilpotent Matrix
    A square matrix A such that Aⁿ = 0 is called a nilpotent matrix of order n.
    If there exists a matrix such that A² = 0, then A is nilpotent of order 2.
    
    • Idempotent Matrix
    A square matrix A, such that A² = A is called an idempotent matrix.
    If AB = A and BA = B, then A and B are idempotent matrices.
    
    • Orthogonal Matrix
    A square matrix A, such that AA^T = l is called an orthogonal matrix.
    If A is an orthogonal matrix, then A^T = A^–1
    
    • Involuntary Matrix
    A square matrix A, such that A² = l is called an involuntary matrix.