Atomic Structure

Synopsis 

Introduction
The phenomenon of static electricity and conduction of electricity through some substances hints at the presence of charged particles in matter.

Discovery of the Electron

• J.J. Thomson performed an experiment by passing electricity at a high voltage through a discharge tube containing a gas at a very low pressure. A green fluorescence was seen emitting out from the other end of the discharge tube.
• This fluorescence is the result of rays emitted from the cathode (negative plate) towards the anode (positive plate) in the discharge tube. Hence, these rays are called cathode rays.
• From his experiment, Thomson arrived at the conclusion that cathode rays are nothing but a stream of negatively charged particles. These negatively charged particles are called electrons.

Discovery of the Proton

• A German scientist, E. Goldstein in 1886, modified the discharge tube and passed electric current through it.
• He found that the positively charged rays were emitted from the anode in the discharge tube. These rays were called canal rays.
• When an electric field was applied, these rays deflected towards the negatively charged plate. Thus, Goldstein concluded that an atom contains positively charged particles along with electrons.
• These positively charged particles were named as protons by a British scientist, Ernest Rutherford.
• Canal rays were also called anode rays since they were emitted from the anode (electrode connected to the positive terminal of high voltage source) in the gas discharge experiments using a perforated cathode.

Discovery of the Neutron

• In 1932, James Chadwick observed that when beryllium was exposed to α-particles, different kinds of particles were emitted.
• These particles had about the same mass as protons and carried no electrical charge. Hence, Chadwick named these particles neutrons.
• These were present in the nucleus along with protons.
• Neutrons are present in the nucleus of all the atoms except hydrogen.
• As protons and neutrons are both present in the nucleus, they are together known as nucleons.

Properties of Electron, Proton and Neutron

The Structure of an Atom

Thomson's Model of an Atom

• Thomson's model of an atom is popularly known as the plum pudding or Christmas pudding model of an atom.
  
  

• According to the Thomson's plum pudding model, an atom is a positively charged sphere in which the electrons are embedded.
• The negative charge of the electrons and the positive charge of the sphere is equal in magnitude. Thus, an atom as a whole is electrically neutral.
• But, his model could not explain the results of experiments carried out by other scientists such as Rutherford and Bohr.

 Limitations of Thomson's Atomic Model

• Although Thomson's atomic model explained why an atom is electrically neutral, it could not explain the distribution of electrons in the atom.
• If we accept that electrons are embedded in the positive charge, then the opposite electric charges should cancel each other out and the charged sphere would be uncharged.
• Thomson's model could not explain why different elements have different chemical properties.

Rutherford's Model of an Atom
In 1911, Earnest Rutherford, a scientist from New Zealand, overturned Thomson’s atomic model by his gold foil experiment.
Rutherford's Atomic Model

• Based on the results of the α-particle scattering experiments, Rutherford put forth his atomic model.
• An atom contains a positively charged centre called the nucleus of the atom. Almost all the mass of the atom is concentrated in the nucleus.
• The electrons of the atom revolve around the nucleus in fixed, circular orbits.
• The size of the nucleus is many times smaller than the size of the atom. The nucleus of an atom is 10,000 times smaller than the atom.
  
   

Drawbacks of Rutherford’s Model of an Atom

• Rutherford’s atomic model could not explain how moving electrons could remain in their orbits.
• Any charged particle during acceleration would radiate energy, and while revolving, it would lose its energy and eventually fall into the nucleus.
• This means that the atom would be highly unstable.
• But, matter is composed of stable atoms.
• Thus, the major drawback of Rutherford’s atomic model was that it could not explain the stability of atoms.
  
    

 Bohr's Model of an Atom

• Niels Bohr, revised Rutherford’s atomic model and put forth the following suggestions:
• Neils Bohr proposed that the electrons possess a specific amount of energy which allows them to revolve around the nucleus.
  
   

• The electrons are confined to these energy levels. While revolving in these discrete orbits, the electrons do not radiate energy. Hence, these orbits are also known as stationary orbits or stationary shells. Smaller the size of the orbit, smaller is its energy.
• As we move away from nucleus, the energy of the orbit increases progressively.
• The transfer of an electron from one orbit to another is always accompanied with absorption or emission of energy.
• When an electron jumps from a lower energy level to a higher energy level, it absorbs energy.
• When an electron returns from a higher energy level to a lower energy level, it emits energy.

• Bohr’s theory for hydrogen atom:

• Stationary states for electron are numbered in terms of principal quantum numbered as n = 1, 2, 3 etc.
• For hydrogen atom: The radii of the stationary states is expressed as r_n = n²a₀ where a₀ = 52.9 pm
• Energy of stationary state

           
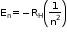
           Where RH= 2.18×10-18 J(Rydbergconstant)
           n= 1,2,3,....
           

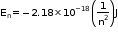
• For ions containing only one electron:
  
  

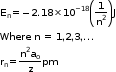
  Where Z is the atomic number.

• Limitations of Bohr’s model of atom:

• It failed to account for the finer details of the hydrogen spectrum. For instance splitting of a line in the spectrum into two closely spaced lines.
• It was also unable to explain spectrum of atoms containing more than one electron.
• It was unable to explain Zeeman effect, i.e. splitting of spectral line in the presence of magnetic effect.
• It also failed to explain Stark effect, i.e. splitting of spectral line in the presence of an electric field.
• It could not explain the ability of atoms to form molecules by chemical bonds.

 Sommerfeld extended Bohr Theory and gave his postulates.

• According to him, the stationary orbits in which electrons are revolving around the nucleus in the atom are not circular but elliptical in shape. It is due to the influence of the centrally located nucleus.
• The electron revolves in elliptical path with nucleus at one of its foci. So there will be a major and a minor axis of the path.
• He said that with the broadening of the orbit, the lengths of the two axis approach to equal value and ultimately become equal i.e. the path become circular. So we can say the circular path is just one special case elliptical path.
• As electrons travel in elliptical path, it will have an angular momentum and this angular momentum must be quantized according to the quantum theory of radiations.
• Bohr gave that angular momentum as m=nh/2𝜋 but Sommerfeld used another integer k instead of n. k is an integer known as azimuthal quantum number. n used by Bohr and k used by Sommerfeld are related as: -

           n/k = length of major axis/length of minor axis

• With increase in value of k, the path becomes more and more elliptical and eccentric. When k=n, the path becomes circular.
• De Broglie’s relation:

• Dual behavior of matter: De Broglie proposed that matter exhibits dual behavior, i.e. matter shows both particle and wave nature.
  
  
• De Broglie’s relation:
  
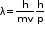
  Where
  - Wavelength
  p - Momentum
  v - Velocity
  h - Planck’s constant

• According to de Broglie, every object in motion has a wave character. Wavelengths of macroscopic objects cannot be detected but for microscopic particles it can be detected.

• Quantum mechanics is a theoretical science that deals with the study of the motion of the microscopic objects that have both observable wave-like properties and particle-like properties.
• When quantum mechanics is applied to macroscopic objects, for which wave like properties are insignificant, the results are the same as those from classical mechanics.
• Quantum mechanics is based on a fundamental equation which is called Schrödinger equation.
• Schrodinger’s equation: For a system such as an atom or a molecule whose energy does not change with time, the Schrödinger equation is written as
  
  Where
  H is the Hamiltonian operator.
  E is the total energy of the system.
  Ψrepresents the wave function which is the amplitude of the electron wave.

• When Schrödinger’s equation is solved for a hydrogen atom, the solution gives the possible energy levels the electrons can occupy and the corresponding wave function(s) of the electron associated with each energy level.
• Ψ gives us the amplitude of wave. The value of y has no physical significance.
• Ψ² gives us the region in which the probability of finding an electron is maximum. It is called probability density.
• Orbital: The region of space around the nucleus where there is maximum probability of finding an electron is called an orbital.
• Quantum numbers: There are a set of four quantum numbers which specify the energy, size, shape and orientation of an orbital.
  These are

• Principal quantum number (n)
• Azimuthal quantum number (l)
• Magnetic quantum number (m_l)
• Electron spin quantum number (m_s)

• Principal quantum number (n): It determines the size and to a large extent the energy of the orbital.
  
  

• It can have positive integer values of 1, 2, 3 and so on.
• It also identifies the shell.
• As the value of n increases, the energy also increases. Hence, the electron will be located far away from the nucleus.

• Azimuthal quantum number (l): The azimuthal quantum number, ‘l’ is also known as orbital angular momentum or subsidiary quantum number. It identified the subshell and the three dimensional shape of the orbital.

• It also determines the number of subshells or sublevels in a shell. The total number of subshells in a particular shell is equal to the value of n.
  l = 0, 1, 2… (n − 1)

• Each subshell corresponding to different values of l are represented by different symbols:
  
  

• Magnetic quantum number or magnetic orbital quantum number (m_l): It gives information about the spatial orientation of the orbital with respect to standard set of coordinate axis.
  For any subshell (defined by ‘l’ value) 2l + 1 values of m_l are possible.
  For each value of l,
  m_l =  −l, − (l − 1), −(l − 2)... 0, 1... (l − 2), (l − 1), l.

• Electron spin quantum number (m_s): It refers to orientation of the spin of the electron. It can have two values +1/2 and −1/2. +1/2 identifies clockwise spin and −1/2 identifies anti-clockwise spin.
• An orbital is identified by a set of 3 quantum numbers: Principal quantum number, azimuthal quantum number and magnetic quantum number.
• An electron is identified by a set of four quantum numbers: Principal quantum number, azimuthal quantum number, magnetic quantum number and spin quantum number.

Shapes of Atomic Orbitals

• An orbital is the three-dimensional space around the nucleus where the probability of finding an electron is maximum. 
• The probability of finding an electron is a function of distance (r) from the nucleus.
• The probability of finding an electron at a distance from the nucleus is called radial probability distribution.
• The region where the probability density function reduces to zero is called radial nodes or nodal surfaces or nodes. 
• Boundary surface diagrams of constant probability density for different orbitals give a fairly good representation of the shapes of the orbitals.
• In this representation, a boundary surface or contour surface is drawn in space for an orbital on which the value of probability density |ψ|2 is constant. In principle, many such boundary surfaces may be possible.
• The s-orbital is spherical, the p-orbital is dumbbell-shaped and the d-orbital is double dumbbell-shaped.
• Let us study each of these orbitals in detail.

 s-Orbital

• For s-orbitals, the number of radial nodes increases with the value of the principal quantum number n and is found to be equal to n − 1.
• The boundary surface diagram for the s-orbital is always a sphere centred on the nucleus irrespective of the principal shell.
   

p-Orbital

The boundary surface diagram for the p-orbital indicates the presence of two lobes which lie on either side of the plane which passes through the nucleus, giving a dumbbell shape to the p-orbital.
The shape suggests that the probability of finding the p-electrons is the maximum within the two lobes. 

p-Orbitals also increase in size and energy with an increase in the principal quantum number. The number of radial nodes for p-orbitals is given by the expression (n − 2); therefore, the number of radial nodes is zero for the 2p-orbital, one for the 3p-orbital and two for the 4p-orbital.

d-Orbital
The probability density function is zero on the plane where the two lobes touch each other. The shape of the d-orbital is double dumbbell. Energy increases with an increase in n.

Total number of nodes for d-orbital          = l + (n − l) − 1
                                                            = n − 1

Total number of nodes for an orbital       = n − 1
Total number of nodes for 3d − orbital    = 3 − 1
                                                           = 2
For d-orbital, l = 2
Number of angular nodes    = l = 2
Number of radial nodes       = (n − l) − 1
                                         = (3 − 2) − 1 = 0

• All the five d-orbitals belonging to a principal shell have the same energies. The size and energies increase with an increase in the principal quantum number.
• Example: The energy of an electron present in 3s, 3p or 3d remains the same irrespective of different values of the Azimuthal quantum number.
  
   

• Radial nodes: Radial nodes occur when the probability density wave function for the electron is zero on a spherical surface of a particular radius. Number of radial nodes = n − l − 1.
• Angular nodes: Angular nodes occur when the probability density wave function for the electron is zero along the directions specified by a particular angle. Number of angular nodes = l.
• Total number of nodes = n − 1.
• Degenerate orbitals: Orbitals having the same energy are called degenerate orbitals.
• Shielding effect or screening effect:  Due to the presence of electrons in the inner shells, the electron in the outer shell will not experience the full positive charge on the nucleus.

So due to the screening effect, the net positive charge experienced by the electron from the nucleus is lowered and is known as the effective nuclear charge.
Effective nuclear charge experienced by the orbital decreases with increase of azimuthal quantum number (l).

• Orbitals have different energies because of mutual repulsion between electrons in a multi-electron atom.
• Orbitals with lower value of (n + l) are filled first as they have lower energy.
• If two orbitals have the same value of (n + l), then orbital with lower value of n will have lower energy.
• Energies of the orbitals in the same subshell decrease with increase in atomic number.
• Filling of electrons: The filling of electrons into the orbitals of different atoms takes place according to Aufbau principle, Pauli’s exclusion principle and Hund’s rule of maximum multiplicity.
• Aufbau principle: In the ground state of the atoms, the orbitals are filled in order of their increasing energies. The order in which the orbitals are filled is as follows
  1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 4f, 5d, 6p, 7s...
  It is based on the (n + l) rule. It states that the orbital with lower value of (n + l) has lower energy.
  
   

• Pauli exclusion principle: No two electrons in an atom can have the same set of four quantum numbers. Only two electrons may exist in the same orbital and these electrons must have opposite spin.

• Electrons with paired spins are denoted by
  
   

• Hund’s rule of maximum multiplicity: Pairing of electrons in the orbitals belonging to the same subshell (p, d or f) does not take place until each orbital belonging to that subshell has got one electron each, i.e. it is singly occupied.

• The configuration of carbon (Z = 6) is 1s2 2s2 2p2. The first four electrons go into the 1s and 2s orbitals. The next two electrons go into separate 2p orbitals, with both electrons having the same spin.
  
   

• Stability of completely filled and half filled subshells:

• Symmetrical distribution of electrons.
• Exchange energy.

Electronic Configuration of Atoms
Distribution of electrons into orbitals of an atom is called its electronic configuration.
To describe the electronic configuration for more than one electron in an atom, we need to know three principles—Pauli exclusion principle, Aufbau principle and Hund’s rule.
The electronic configuration of different atoms can be represented in two ways.
Example:

1.   s^a  p^b  d^c (notations)
2.   Orbital diagram

• In the first case, the subshell is represented by the respective letter symbol. The number of electrons present in the subshell is depicted as a superscript such as a, b, c,....
• The similar subshell represented for different shells is differentiated by writing the principal quantum number before the respective subshell.
• In the second case, each orbital of the subshell is represented by a box and the electron is represented by an upward arrow (↑) (a positive spin) or a downward arrow (↓) (a negative spin).
  

• The advantage of the second notation over the first is that it represents all the four quantum numbers.
• The hydrogen atom has only one electron which goes in the orbital with the lowest energy, namely 1s.
• The electronic configuration of the hydrogen atom is 1s¹, meaning that it has one electron in the 1s orbital.
• The second electron in helium (He) can also occupy the 1s orbital. Its configuration is 1s². As mentioned above, the two electrons differ from each other
  with opposite spin, as can be seen from the orbital diagram.
  (Refer to the figure below)
  
  
  
  
• The third electron of lithium (Li) is not allowed in the 1s orbital because of Pauli’s exclusion principle.

It therefore takes the next available choice, namely, the 2s orbital.

• The electronic configuration of Li is 1s² 2s¹.
• The 2s orbital can accommodate one more electron.
• The configuration of beryllium (Be) atom is therefore 1s² 2s².
• In the next six elements—boron (B, 1s²2s²2p¹), carbon (C, 1s²2s²2p²), nitrogen (N, 1s²2s²2p³), oxygen (O, 1s²2s²2p⁴), fluorine (F, 1s²2s²2p⁵) and neon (Ne, 1s²2s²2p⁶), the 2p orbitals get progressively filled.
• This process is completed with the neon atom. The orbital picture of these elements can be represented as follows:
  
  

• The electronic configuration of the elements sodium (Na, 1s² 2s² 2p⁶ 3s¹) to argon (Ar,1s² 2s² 2p⁶ 3s² 3p⁶) follows exactly the same pattern as the elements from lithium to neon with the difference that the 3s and 3p orbitals are getting filled now. This process can be simplified if we represent the total number of electrons in the first two shells by the name of the noble gas element neon (Ne).
• The electronic configuration of the elements from sodium to argon can be written as (Na, [Ne] 3s¹) to (Ar, [Ne] 3s²3p⁶).
• Electrons in the completely filled shells are known as core electrons, and electrons which are added to the electronic shell with the highest principal quantum number are called valence electrons.

Example:
Electrons in Ne are core electrons, and electrons from Na to Ar are valence electrons.
In potassium (K) and calcium (Ca), the 4s orbital, being lower in energy than the 3d orbitals, is occupied by one and two electrons, respectively.

• A new pattern is followed beginning with scandium (Sc). The 3d orbital, being lower in energy than the 4p orbital, is filled first.
• Consequently, in the next ten elements—scandium (Sc), titanium (Ti), vanadium (V), chromium (Cr), manganese (Mn), iron (Fe), cobalt (Co), nickel (Ni), copper (Cu) and zinc (Zn), the five 3d orbitals are progressively occupied.
• With the saturation of the 3d orbitals, the filling of the 4p orbital starts at gallium (Ga) and is complete at krypton (Kr).
• In the next eighteen elements from rubidium (Rb) to xenon (Xe), the pattern of filling the 5s, 4d and 5p orbitals is similar to that of 4s, 3d and 4p orbitals as discussed above.
• Then comes the turn of the 6s orbital.
• In caesium (Cs) and barium (Ba), this orbital contains one and two electrons, respectively.
• Then from lanthanum (La) to mercury (Hg), the filling of electrons takes place in 4f and 5d orbitals.
• After this, filling of 6p, then 7s and finally 5f and 6d orbitals takes place.
• The elements after uranium (U) are short-lived and all of them are produced artificially.
• The electronic configurations of the known elements (as determined by spectroscopic methods).

Stability of Completely Filled and Half-Filled Subshells

• The ground state electronic configuration of the atom of an element always corresponds to the state of the lowest total electronic energy.
• The electronic configurations of most atoms follow the basic rules.
• However, in certain elements such as Cu or Cr, where the two subshells (4s and 3d) differ slightly in their energies, an electron shifts from a subshell of lower energy (4s) to a subshell of higher energy (3d), provided such a shift results in all orbitals of the subshell of higher energy getting either completely filled or half-filled.
• Therefore, the valence electronic configurations of Cr and Cu are 3d⁵ 4s¹ and 3d¹⁰ 4s¹, respectively and not 3d⁴ 4s² and 3d⁹ 4s².
• There is extra stability associated with these electronic configurations.