CBSE Class 11-science Answered
Q. Prove that the lines (b-c)x+(c-a)y+(a-b)=0, (c-a)x+(a-b)y+(b-c)=0 and (a-b)x+(b-c)y+(c-a)=0 are concurrent.
Asked by imabhi264 | 28 Dec, 2017, 18:31: PM

Answered by Sneha shidid | 31 Dec, 2017, 19:35: PM
Concept Videos
CBSE 11-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 13:23: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 20 Oct, 2016, 06:34: AM
CBSE 11-science - Maths
Asked by Topperlearning User | 29 Apr, 2014, 15:09: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 20 Oct, 2016, 06:32: AM
CBSE 11-science - Maths
Asked by Topperlearning User | 28 Apr, 2014, 08:04: AM
CBSE 11-science - Maths
Asked by Topperlearning User | 30 Apr, 2014, 09:00: AM
CBSE 11-science - Maths
Asked by Topperlearning User | 30 Apr, 2014, 09:03: AM
CBSE 11-science - Maths
Asked by Topperlearning User | 30 Apr, 2014, 09:08: AM
CBSE 11-science - Maths
Asked by Topperlearning User | 20 Oct, 2016, 06:26: AM
CBSE 11-science - Maths
Asked by Topperlearning User | 20 Oct, 2016, 06:20: AM

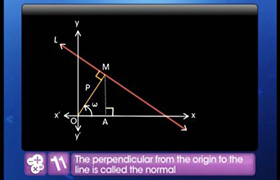


 5y + 23 = 0 and passing through the point (3, -5).
5y + 23 = 0 and passing through the point (3, -5).