Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 11-science Answered

Find the coordinates of the foot of the perpendicular from the point (3, -4) to the line 4x - 15y + 17 = 0.
Asked by Topperlearning User | 30 Apr, 2014, 09:00: AM
Expert Answer

The equation of the given line is 4x - 15y + 17 =   0            ...  (i)

The equation of a line perpendicular to the given line is 15x + 4y - k = 0, where k is a constant.
If this line passes through the point (3, -4), then
            15 x 3 + 4 x (-4) - k = 0
          45 - 16 - k = 0
        k = 29
Therefore the equation of a line passing through the point (3, -4) and perpendicular to the given line is
15x + 4y - 29 = 0                                         ...    (ii)

        The required foot of the perpendicular is the point of intersection of lines (i) and (ii).
Solving equation (i) and (ii), we get

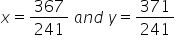
x equals 367 over 241 space a n d space y equals 371 over 241
Therefore, the foot of the perpendicular is given by

open parentheses 367 over 241 comma space 371 over 241 close parentheses
Answered by | 30 Apr, 2014, 11:00: AM

Concept Videos

Multiple Choice Questions Practice Test Subjective Questions Webinar Subjective Questions Pre Board Assessment
Answered Unanswered My Questions My Answers
CBSE 11-science - Maths
Find the equation of a line whose perpendicular distance from the origin is 6 units and the angle made by the perpendicular with positive x-axis is 60°.
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERT
CBSE 11-science - Maths
Reduce the equation 4x + 3y – 9 = 0 to the normal form and find their length of perpendicular from origin to the line
Asked by Topperlearning User | 20 Oct, 2016, 06:34: AM
ANSWERED BY EXPERT
CBSE 11-science - Maths
Find the distance of the point (2, 5) from the line 4 (x + 5) = 7 (2y - 3).
Asked by Topperlearning User | 29 Apr, 2014, 03:09: PM
ANSWERED BY EXPERT
CBSE 11-science - Maths
Find the distance between the parallel lines 3x + 5y + 13 = 0 and 3x + 5y – 24 = 0.
Asked by Topperlearning User | 20 Oct, 2016, 06:32: AM
ANSWERED BY EXPERT
CBSE 11-science - Maths
Find the equation of the line parallel to the line 24x minus5y + 23 = 0 and passing through the point (3, -5).
Asked by Topperlearning User | 28 Apr, 2014, 08:04: AM
ANSWERED BY EXPERT
CBSE 11-science - Maths
Find the coordinates of the foot of the perpendicular from the point (3, -4) to the line 4x - 15y + 17 = 0.
Asked by Topperlearning User | 30 Apr, 2014, 09:00: AM
ANSWERED BY EXPERT
CBSE 11-science - Maths
Find the equation of the line perpendicular to the line 2x - 3y + 7 = 0 and having x-intercept 4.
Asked by Topperlearning User | 30 Apr, 2014, 09:03: AM
ANSWERED BY EXPERT
CBSE 11-science - Maths
If p and q are the lengths of perpendicular from the origin to the lines x cos q - y sin q = k cos 2 q and x sec q + y cosec q = k respectively. Prove that p2 + 4q2 = k2.
Asked by Topperlearning User | 30 Apr, 2014, 09:08: AM
ANSWERED BY EXPERT
CBSE 11-science - Maths
Find the points on the y-axis, whose distances from the line  are 5 units.
Asked by Topperlearning User | 20 Oct, 2016, 06:26: AM
ANSWERED BY EXPERT
CBSE 11-science - Maths
Find the distance between the parallel lines m (x + y) – n = 0 and mx + my + r = 0.
Asked by Topperlearning User | 20 Oct, 2016, 06:20: AM
ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt