CBSE Class 11-science Answered
The frequency 'n' of vibration of stretched string depends on its length 'L' its mass per unit length 'm' and the tension 'T' in the string obtain dimensionally an expression for frequency 'n'.
Asked by jullypradhan001 | 05 Aug, 2018, 11:48: PM
Expert Answer
Frequency is denoted by 'n'
let us consider
n= klxTymz ...(1)
Writing dimension for each quantity,
n → [M0L0T -1]
l→ [M0L1T0]
T→[M1L1T-2]
m→[M1L-1T0]
Substituting dimensions in equation (1),
[M0L0T-1] = k[M0L1T0]x [M1L1T-2]y [M1L-1T0]z
[M0L0T-1] = k [My+z Lx+y-z T-2y] ...(2)
From (2),
y+z = 0
x+y-z =0
-2y = -1 ....(3)
Solving equations (3) simultanously we get,
x = -1, y = 1/2 and z = -1/2
Substituting these value of x,y and z in equation (1),
n= kl-1T1/2m-1/2
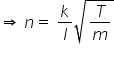
This is the formula for frequency of vibration for stretched string.
Answered by Shiwani Sawant | 06 Aug, 2018, 12:18: PM
CBSE 11-science - Physics
Asked by snehasahu824 | 03 Mar, 2020, 10:06: AM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by devvratagrahari | 02 Dec, 2019, 06:44: AM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by SELVA | 06 Jul, 2019, 03:25: PM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by Vidushi412 | 14 Jan, 2019, 09:43: PM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by jullypradhan001 | 05 Aug, 2018, 11:48: PM
ANSWERED BY EXPERTCBSE 11-science - Physics
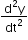+ ky = 0, what is the time period of motion?Asked by Topperlearning User | 15 May, 2015, 10:54: AM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by Topperlearning User | 15 May, 2015, 10:00: AM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERT
