CBSE Class 11-science Answered
when an object is subjected to a restoring force F that is proportional to displacement,
then the object is undergoing simple harmonic motion.
Let m be the mass of the object .
If restoring force F is proportional to displacement x , then it is mathemetically written as
F ∝ x
F = - k x ( negative sign is used because force is restoring force )
where k is proportionality constant and it is known as force constant
force F = mass × acceleration
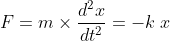
Above expression can be written as
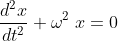 .........................(1)
.........................(1)
where ω2 = k/m .
For above second order differential equation , the solution is written as
x = a cos(ωt) + b sin(ωt) ......................(2)
where a and b are constants ,
If we choose the constants so that
a/b = tan φ ; a = A cos φ ; b = A sin φ
then eqn.(2) will be written as
x = A [ cosφ cos(ωt)+ sinφ sin(ωt)]
x = A cos( ωt - φ )
where A is amplitude , ω is angular frequency and φ is initial phase at t = 0




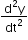 + ky = 0, what is the time period of motion?
+ ky = 0, what is the time period of motion?