CBSE Class 10 Answered
PQRS is a circle and circles are drawn with PO, QO, RO and SO as diameters areas A and B are shaded A/B is equal to
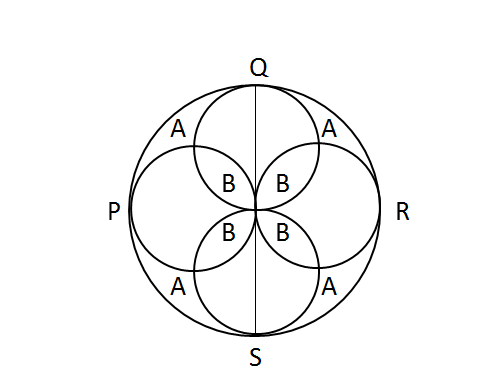
Asked by rushabh123 | 07 Feb, 2019, 10:15: AM
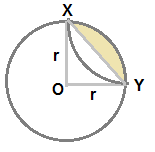
Let r be the radius of small circles given in the quetion-figure.
The marked area as B in the figure given in question is twice the shaded area shown in above figure.
Shaded area shown in above figure = Area of quarter circle - area of triangle OXY = (π/4)r2 - (1/2)r2 = [ (π-2)/4 ]r2
Hence marked area as B in the question-figure = [ (π-2)/2 ]r2 ......................(1)
marked area as A in question-figure = (1/4)[ area of outer circle - { (4×area of inner circle) - (all the areas marked as B) } ]
marked area as A in question-figure = (1/4)[ π(2r)2 - (4×πr2) + 4×{ (π-2)/2 }r2 ] = [ (π-2)/2 ]r2 ............(2)
By comparing eqn.(1) and eqn.(2), we see the area marked as A is same as the area marked as B.
Hence the required ratio of areas = 1
Answered by Thiyagarajan K | 07 Feb, 2019, 01:32: PM
Application Videos
Concept Videos
CBSE 10 - Maths
Asked by laxman44verma | 01 May, 2024, 09:46: PM
CBSE 10 - Maths
Asked by dagardisha39 | 28 Apr, 2024, 12:58: PM
CBSE 10 - Maths
Asked by raopaidi | 25 Apr, 2024, 04:06: PM
CBSE 10 - Maths
Asked by aditikaldate7 | 21 Apr, 2024, 03:16: PM
CBSE 10 - Maths
Asked by pathaksuman622 | 21 Apr, 2024, 11:56: AM
CBSE 10 - Maths
Asked by yalagondanikhil | 16 Apr, 2024, 12:25: PM
CBSE 10 - Maths
Asked by rrajansinghakb199 | 08 Apr, 2024, 05:12: PM
CBSE 10 - Maths
Asked by nagalaxmidurgarao937 | 08 Apr, 2024, 01:42: PM
CBSE 10 - Maths
Asked by mraniruddha03 | 02 Apr, 2024, 06:44: PM
CBSE 10 - Maths
Asked by muttenenimalleswarrao | 29 Mar, 2024, 08:32: PM












