CBSE Class 10 Answered
In the figure, a square is inscribed in a circle of diameter d and another square
is circumscribing the circle. Find the ratio of the area of the outer square to the
area of the inner square.
Asked by dhruvshrotriya03 | 28 Feb, 2019, 07:36: PM
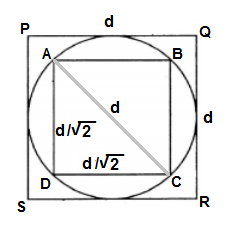
side of outer square equals to diameter of circle d. Hence area of outer square PQRS = d2 sq.units
diagonal of square ABCD is same as diameter of circle. Hence side of square ABCD d/√2 units . Hence area of ABCD = d2/2
Ratio of area of outer square to the area of inner square = 

Answered by Thiyagarajan K | 28 Feb, 2019, 10:51: PM
Application Videos
Concept Videos
CBSE 10 - Maths
Asked by laxman44verma | 01 May, 2024, 09:46: PM
CBSE 10 - Maths
Asked by dagardisha39 | 28 Apr, 2024, 12:58: PM
CBSE 10 - Maths
Asked by raopaidi | 25 Apr, 2024, 04:06: PM
CBSE 10 - Maths
Asked by aditikaldate7 | 21 Apr, 2024, 03:16: PM
CBSE 10 - Maths
Asked by pathaksuman622 | 21 Apr, 2024, 11:56: AM
CBSE 10 - Maths
Asked by yalagondanikhil | 16 Apr, 2024, 12:25: PM
CBSE 10 - Maths
Asked by rrajansinghakb199 | 08 Apr, 2024, 05:12: PM
CBSE 10 - Maths
Asked by nagalaxmidurgarao937 | 08 Apr, 2024, 01:42: PM
CBSE 10 - Maths
Asked by mraniruddha03 | 02 Apr, 2024, 06:44: PM
CBSE 10 - Maths
Asked by muttenenimalleswarrao | 29 Mar, 2024, 08:32: PM












