CBSE Class 10 Answered
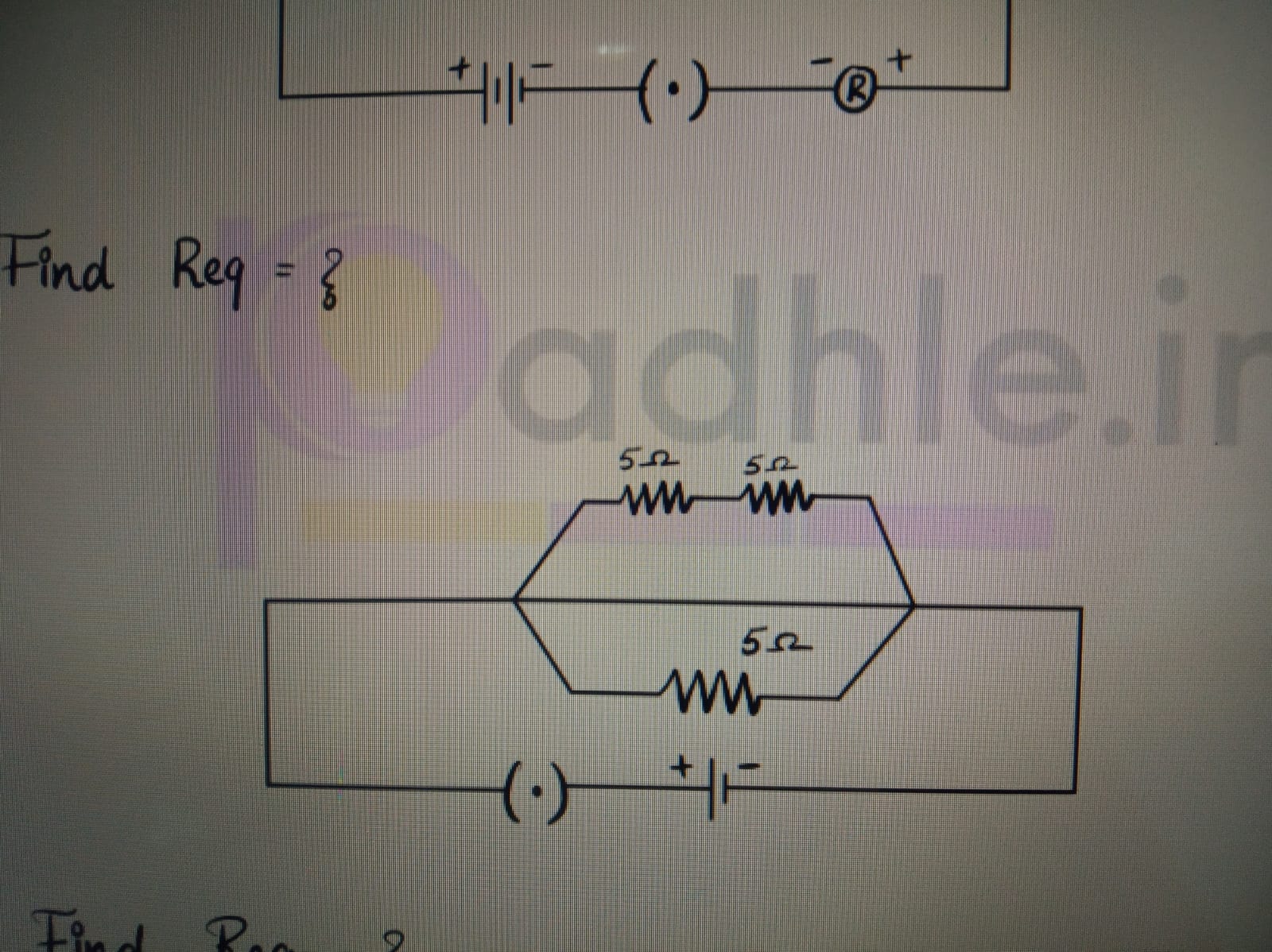
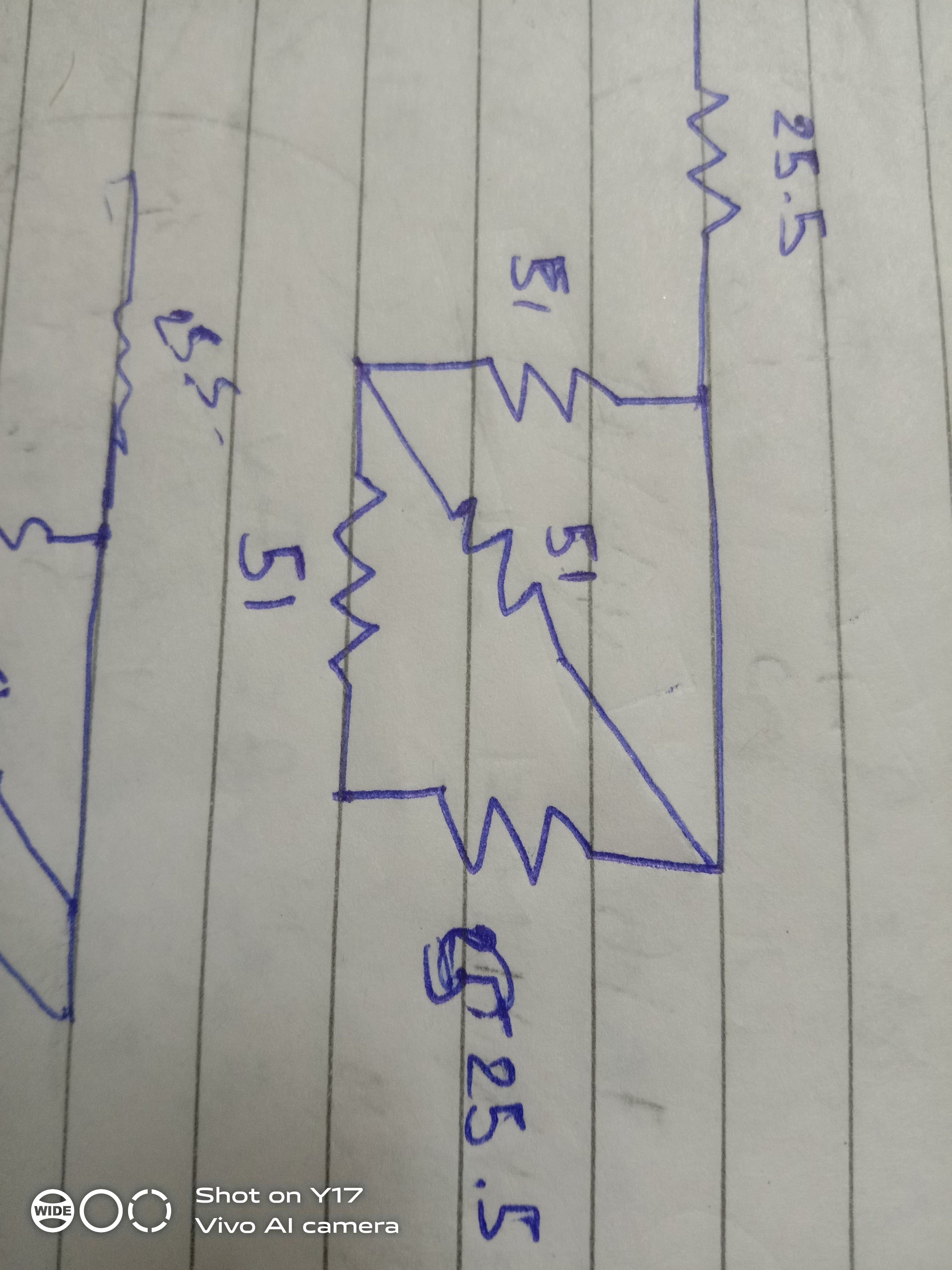
how to calculate the resistance if the resistors are inclined between parallel wires

Asked by acshanadhana15 | 18 Oct, 2020, 19:21: PM
For such problems,
We will start solving from right side.
In circuit diagram,
R8 and R10 are in series with each other while R9 is in parallel to them
Thus,
Rs = 10 + 2 = 12 Ω
and
1/Rp = (1/ Rs) + (1/R9) = (1/12) + (1/6)
Thus,
Rp = 4 Ω
Let this combination of resistors R8, R9 and R10 be named as Ra
The resistor R7 is in resistor with Ra
Thus,
Ra + R7 = 4 + 8 = 12 Ω
R6 is in parallel to this whole combination and let us name this whole combination as Rb
Thus,
1/Rb = (1/R6) + (1/12) = (1/6) + (1/12)
Rb = 4 Ω
From circuit diagram
Rb ad R5 is in series,
Thus,
Rb + R5 = 4 + 4 = 8 Ω
R4 is in paralell to this combination and let the resistance be Rc
Thus,
1/Rc = (1/8) + (1/ 8)
Rc = 4 Ω
Rc and R3 are in series
Thus,
Rc + R3 = 4 + 4 = 8 Ω
This 8 ohms is in parallel with R2 and can be named as Rd
Thus,
1/Rd = (1/8) + (1/R2) = (1/8) + (1/8)
Rd = 4 Ω
Rd is in series with R1
Thus,
Req = Rd + R1 = 4 + 6 = 10 Ω
Answered by Shiwani Sawant | 19 Oct, 2020, 14:45: PM
Application Videos
Concept Videos
CBSE 10 - Physics
Asked by kamalaranjanmohantymohanty5 | 06 Jan, 2024, 10:05: AM
CBSE 10 - Physics
Asked by nandhikasugumar | 05 Oct, 2023, 16:01: PM
CBSE 10 - Physics
Asked by daniya062008 | 02 Oct, 2023, 20:25: PM
CBSE 10 - Physics
Asked by prassanna.j | 03 Sep, 2023, 12:28: PM
CBSE 10 - Physics
Asked by prassanna.j | 03 Sep, 2023, 12:21: PM
CBSE 10 - Physics
Asked by prassanna.j | 03 Sep, 2023, 12:11: PM
CBSE 10 - Physics
Asked by prassanna.j | 28 Aug, 2023, 21:49: PM
CBSE 10 - Physics
Asked by praveenkumae975 | 06 Feb, 2023, 19:19: PM