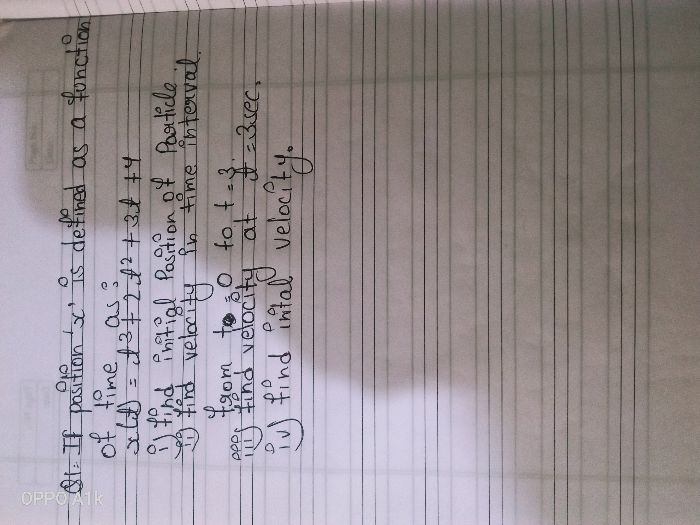CBSE Class 11-science Answered
Here in question 3 I am unable to get the velocity from the derivative. Please show me how the velocity is obtained.
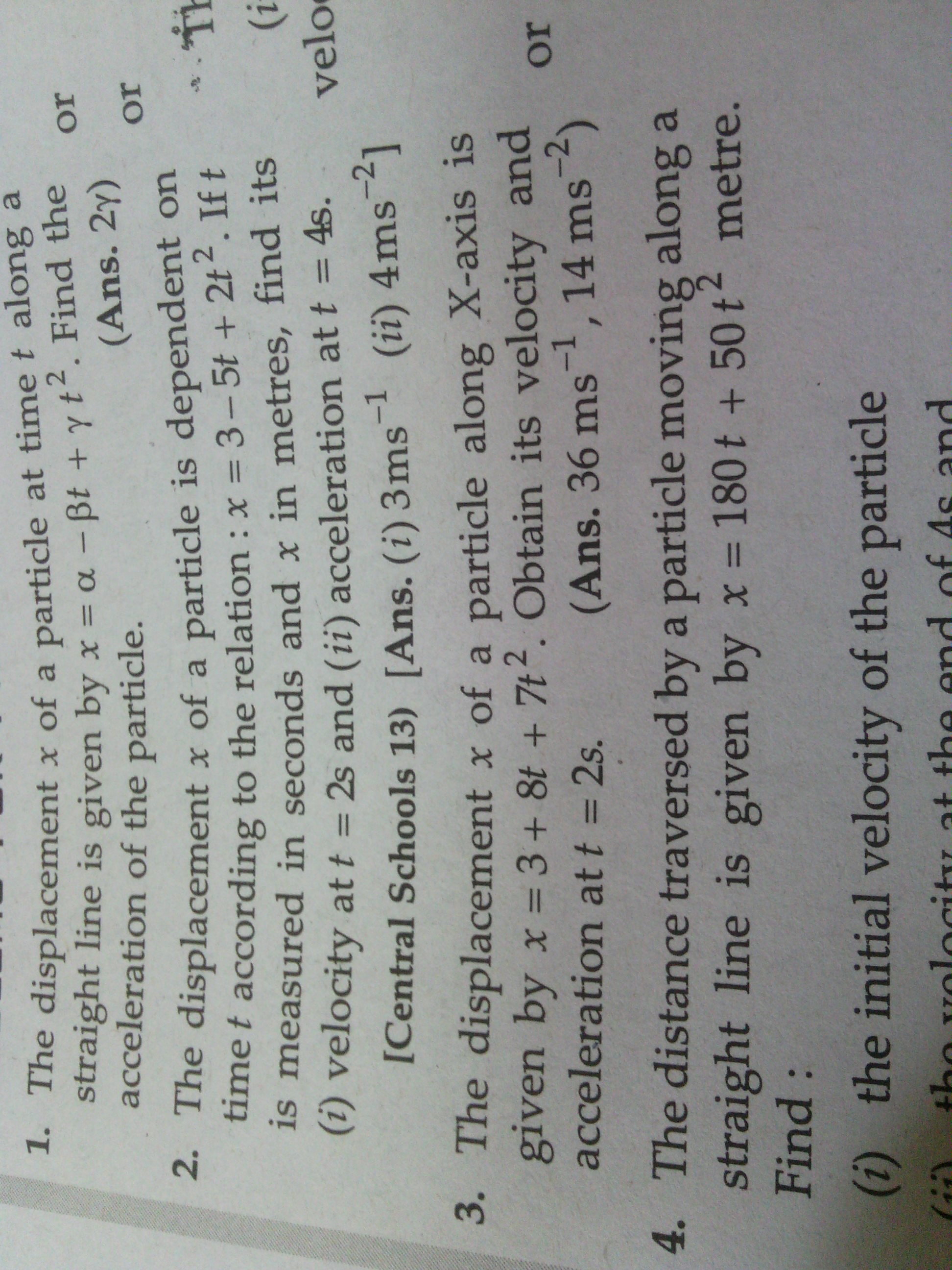
Asked by Varsneya Srinivas | 02 Jul, 2016, 09:39: AM
We know that velocity is the rate of change of displacemnet.
Given that

Answered by Yashvanti Jain | 04 Jul, 2016, 10:30: AM
Concept Videos
CBSE 11-science - Physics
Asked by manjusrihalder395 | 07 Jan, 2024, 09:55: PM
CBSE 11-science - Physics
Asked by spandya632 | 17 Nov, 2023, 08:36: AM
CBSE 11-science - Physics
Asked by hy9022075 | 10 Jan, 2023, 09:06: PM
CBSE 11-science - Physics
Asked by ad4957216 | 03 Jan, 2023, 04:54: PM
CBSE 11-science - Physics
Asked by prashantgaikwadfox000 | 25 Sep, 2022, 05:38: PM
CBSE 11-science - Physics
Asked by ukalyadab | 18 Jul, 2022, 11:52: AM
CBSE 11-science - Physics
Asked by piyushhoney2006 | 20 Jun, 2022, 04:12: PM
CBSE 11-science - Physics
Asked by chinttubabu9692 | 27 Jan, 2022, 06:37: PM