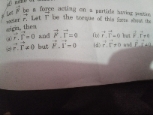CBSE Class 11-science Answered

As the string winds around the peg, the radius of rotation of the particle decreases, causing a decrease in the moment of inertia of the particle.

Here momentum is conserved and, as the moment of inertia of the particle decreases, its speed increases.( Recall that v = ωr).

Thus the initial angular velocity of the particle,

ω₀ = v/r = 3 rad/s

The initial moment of inertia of the particle is,

 I₀ = mR ² = 4m 

 We want to find r , the radius of the string when the particle has a speed of 20 m/s.

At this point, the angular velocity of the particle is,

ω_f = v/r = 20/r

The moment of inertia =  I_f = mr² 

Now apply the conservation of angular momentum to find our value for r.

Initial angular momentum = final angular momentum

I₀ω₀ = I_fω_f

(4m) × 3 = mr² × 20/r

12 = 20 r

r = 0.6 m