Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

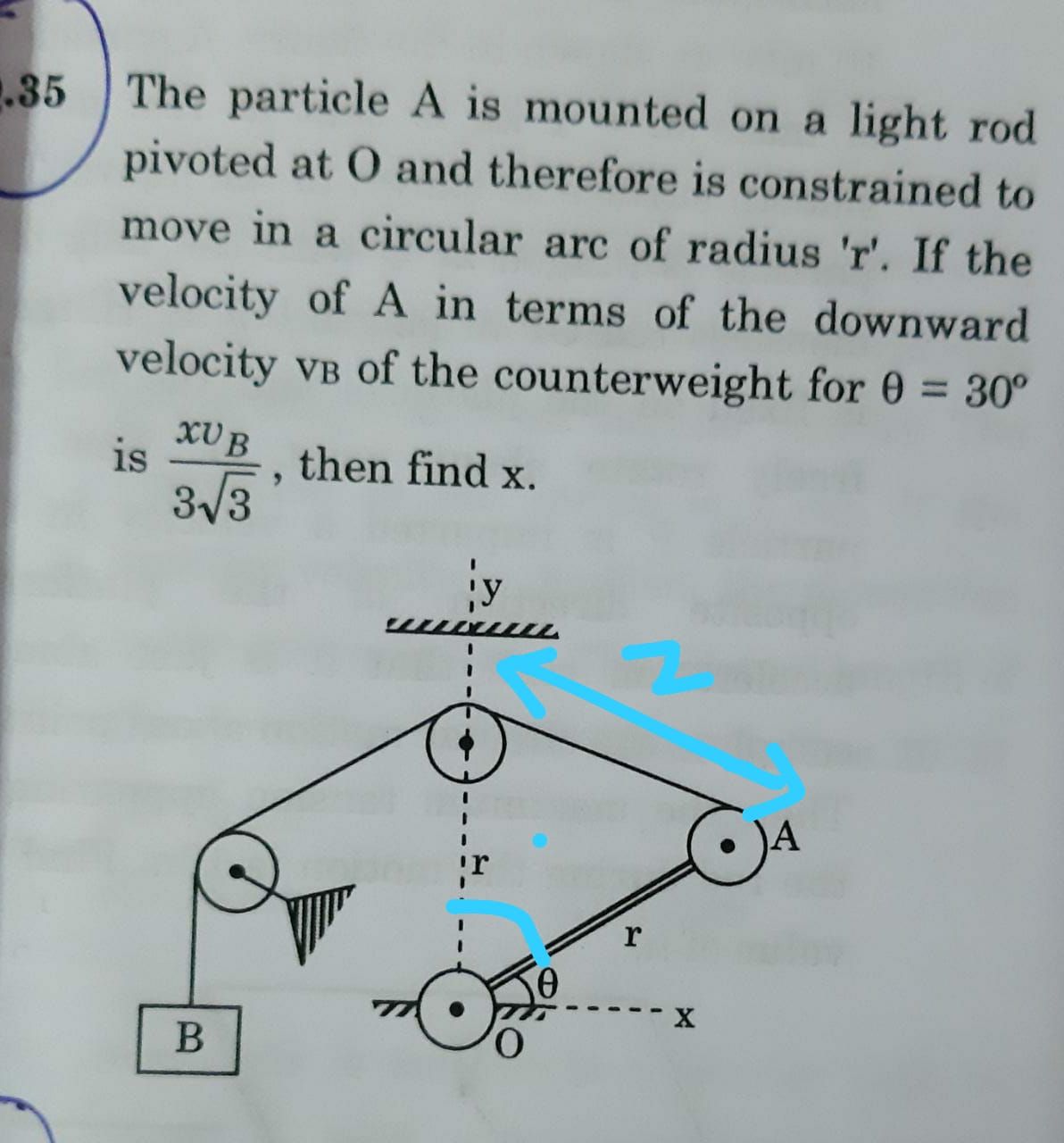
CBSE Class 11-science Answered

one meter long string can bear maximum of 0.5 kg mass . a mass of 0.05 kg is tied to one end and rotated in a horizontal circle , calculate the maximum number of revolution so that string does not brakes
Asked by pushpakumari291279 | 20 Aug, 2022, 08:15: AM
answered-by-expert Expert Answer
Maximum Tension force Tmax that is bearable by string = M g
 
where M is mass hanging to give tension force in the string and g is acceleration due to gravity
 
Tension force F experienced by string, when it is attached to mass m and is revolved horizontally is given as
 
F = m ω2 L
 
where ω is angular speed of revolution and L is length of string
 
For maximum revolution speed , we have ,  F = Tmax
 
m ω2 L = M g
 
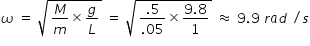
begin mathsize 14px style omega space equals space square root of M over m cross times g over L end root space equals space square root of fraction numerator.5 over denominator.05 end fraction cross times fraction numerator 9.8 over denominator 1 end fraction end root space almost equal to space 9.9 space r a d space divided by s end style
Number of revolution per second = 9.9 / ( 2 π )  ≈ 1.57
 
Number of revolution per minute  = 1.57 × 60  ≈ 94
Answered by Thiyagarajan K | 20 Aug, 2022, 11:31: AM

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 11-science - Physics
one meter long string can bear maximum of 0.5 kg mass . a mass of 0.05 kg is tied to one end and rotated in a horizontal circle , calculate the maximum number of revolution so that string does not brakes
Asked by pushpakumari291279 | 20 Aug, 2022, 08:15: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
 solve this question
question image
Asked by Vipulgautam050 | 26 Aug, 2021, 08:57: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
On a toy comprising of a disc of radius 4 m, a bird is sitting on the periphery (the outer edge). Find the instantaneous velocity of the bird if disk is rotating at 180 revolutions per minute.
Asked by Topperlearning User | 11 Aug, 2014, 11:03: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
Fly wheel rotates at a speed of 360 rpm and at a rate of 6 rad /s2 it slows down. Calculate the time after which it will stop.
Asked by Topperlearning User | 11 Aug, 2014, 11:06: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
A nail punctures a tyre , the speed of tyre reduces from 240rpm to 120rpm in 6sec. Find the angular acceleration. Is it acceleration or deceleration?
Asked by Topperlearning User | 11 Aug, 2014, 12:32: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
A musical record of 200gm has a radius of 10cm.We apply a torque of 0.1 Nm .Find the angular acceleration.
Asked by Topperlearning User | 11 Aug, 2014, 11:11: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
Moment of inertia in rotational motion is an analogue of a physical quantity in linear motion. Name the quantity.
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
If the angular position of a body under circular motion is given by the equation: Find the expression for angular velocity and angular displacement.
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
Ram tied a stone at the end of a thread. In 10 s with a uniform angular acceleration he rotates the stone from a speed of 120 rpm to a speed of 180 rpm. Find the angular acceleration and angular displacement.
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
What is the unit of rotational displacement?
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×