CBSE Class 11-science Answered
A hollow sphere of mass m and radius R is rolling downward on a rough inclined plane of inclination 0 (theta) . if the coefficient of friction between the hollow sphere and incline is µ then
1. Friction opposes its translation
2. Friction supports rotation motion
3. on decreasing 0 (theta), frictional force decreases
4. all of these.
Pleae provide justification
Asked by Sayoni Maiti | 13 Oct, 2014, 12:21: AM
Expert Answer
The answer to this is 4.all of these.
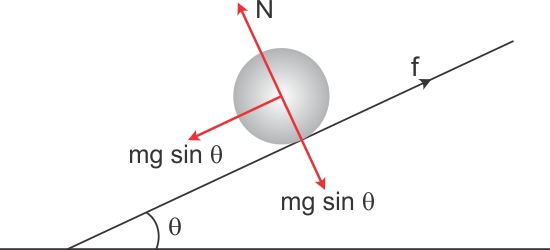
When a body is placed on an inclined plane at an angle θ, it tries to slip down and hence a static friction 'f' acts upwards. Thus it opposes the translational motion. This friction provides a torque which causes the body to rotate.Frictional force provides the torque for rotation. Hence we can say that the friction supports rotational motion.
If μ is the minimum coefficient of friction between the hollow sphere and the incline plane .From the motion of hollow sphere we can write that
mg sin θ - f =ma
where a is the acceleration along the incline plane(i.e. tangential acceleration of the rolling sphere)
f - static friction acting upwards
θ- inclination angle.
From all the above we can say that the frictional force decreases on decreasing θ.
Answered by Jyothi Nair | 13 Oct, 2014, 11:14: AM
Concept Videos
-
Systems of Particles and Rotational Motion
This video explains the nature of a rigid body, the centre of mass, the mot... -
Systems of Particles and Rotational Motion
This video explains torque, magnitude of torque and the right hand rule on ... -
Systems of Particles and Rotational Motion
This video explains the moment of inertia, its relation with rotational kin... -
Systems of Particles and Rotational Motion
This video explains the analogy between linear and angular variables of mot... -
Systems of Particles and Rotational Motion
This video explains the analogy between the torque of rotational and linear...
CBSE 11-science - Physics
Asked by rustampathan | 25 Feb, 2024, 06:39: PM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by gipaalsy | 08 Feb, 2024, 05:41: AM
ANSWERED BY EXPERT
CBSE 11-science - Physics
Asked by priyankaprajapti81 | 04 Nov, 2023, 10:47: PM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by gdeadshot85 | 14 Jan, 2023, 09:58: PM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by devanshchauhan325 | 23 Dec, 2022, 07:34: AM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by koushtubhroy | 20 Dec, 2022, 07:36: AM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by pushpakumari291279 | 20 Aug, 2022, 08:15: AM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by adipadmakarri | 26 Sep, 2021, 06:08: PM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by adipadmakarri | 25 Sep, 2021, 11:18: AM
ANSWERED BY EXPERT
