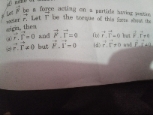CBSE Class 11-science Answered
A hollow sphere is released from rest on a rough inclined plane as shown in the figure. Find the velocity of point of contact as a function of time. (m=mass of hollow sphere,R=radius of sphere)

Asked by everyteengamer | 29 Feb, 2020, 11:17: AM
Let us find acceleration due to slipping
As shown in figure, net force acting on hollow sphere = ( mg sin37 - μ mg cos37 )
Hence , acceleration = force / mass = g ( sin 37 - μ cos 37 ) = 9.8 ( 0.6 - 0.2 × 0.8 ) = 4.312 m/s2
Let us find acceleration due to rolling
friction force gives a torque τ to rotate the hollow sphere
we have , τ = I α ................(1)
where I is moment of inertia , I = (2/3)mR2 , where R is radius of hollow sphere and α is angular acceleration
Torque τ = force × perpendicular distance = μ mg cos37 × R .............(2)
from (1) and (2), we have, μ mg cos37 × R = (2/3)mR2 × α ..............(3)
By substituting values for μ and g , we get after simplification, α = 2.352 / R
Hence linear acceleration a = α × R = 2.352 m/s2
At point of contact acceleration due to slipping is downward , but acceleration due to rolling is in upward direction so that
it is opposite to the direction of acceleration due to slipping.
Hence net acceleration = ( 4.312 - 2.352 ) m/s2 = 1.96 m/s2
velocity of point of contact as a function of time = acceleration × time = 1.96 t m/s ≈ 2 t m/s
Answered by Thiyagarajan K | 29 Feb, 2020, 06:40: PM
Concept Videos
CBSE 11-science - Physics
Asked by rustampathan | 25 Feb, 2024, 06:39: PM
CBSE 11-science - Physics
Asked by gipaalsy | 08 Feb, 2024, 05:41: AM
CBSE 11-science - Physics
Asked by priyankaprajapti81 | 04 Nov, 2023, 10:47: PM
CBSE 11-science - Physics
Asked by gdeadshot85 | 14 Jan, 2023, 09:58: PM
CBSE 11-science - Physics
Asked by devanshchauhan325 | 23 Dec, 2022, 07:34: AM
CBSE 11-science - Physics
Asked by koushtubhroy | 20 Dec, 2022, 07:36: AM
CBSE 11-science - Physics
Asked by pushpakumari291279 | 20 Aug, 2022, 08:15: AM
CBSE 11-science - Physics
Asked by adipadmakarri | 26 Sep, 2021, 06:08: PM
CBSE 11-science - Physics
Asked by adipadmakarri | 25 Sep, 2021, 11:18: AM