Relations
Relation Synopsis
Synopsis
Ordered pairs
- A pair of elements grouped together in a particular order is known as an ordered pair.
- The two ordered pairs (a, b) and (c, d) are said to be equal if and only if a = c and b = d.
Cartesian product of two or more sets
- Let A and B be any two non-empty sets. The Cartesian product A × B is the set of all ordered pairs of elements from the sets A and B defined as follows:
- A × B = {(a, b): aÎ A, bÎ B}.
- Cartesian product of two sets is also known as the product set.
- Cartesian product of sets can be extended to three or more sets. If A, B and C are three non-empty sets, then A × B × C = {(a, b, c): a Î A, b Î B, c Î C}. Here (a, b, c) is known as an ordered triplet.
- Cartesian product of a non-empty set A with an empty set is an empty set, i.e. A × Φ = Φ.
Number of elements in Cartesian product
- If any of the sets of A or B or both are empty, then the set A × B will also be empty and consequently, n(A × B) = 0.
- If the number of elements in A is m and the number of elements in set B is n, then the set A × B will have mn elements.
- If any of the sets A or B is infinite, then A × B is also an infinite set.
Laws of algebra on Cartesian product
- The Cartesian product is not commutative, namely A × B is not the same as B × A, unless A and B are equal.
- The Cartesian product is associative, namely A × (B × C) = (A × B) × C
- R × R = {(a, b) : a Î R, b Î R} represents the coordinates of all points in the two-dimensional plane.
- R × R × R = {(a, b, c) : a Î R, b Î R, c Î C} represents the coordinates of all points in the three dimensional plane.
Relation
- A relation R from a non-empty set A to another non-empty set B is a subset of their Cartesian product A × B, i.e. R Î A × B.
- If (x, y) Î R or x R y, then ‘x’ is related to ‘y’.
- If (x, y)
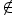 R or x R y, then ‘x’ is not related to ‘y’.
R or x R y, then ‘x’ is not related to ‘y’. - The second element b in the ordered pair (a, b) is the image of the first element a, and a is the pre-image of b.
Domain, co-domain and range of a relation
- The domain of R is the set of all first elements of the ordered pairs in a relation R. In other words, the domain is the set of all the inputs of the relation.
- If the relation R is from a non-empty set A to non-empty set B, then set B is called the co-domain of the relation R.
- The set of all the images or the second element in the ordered pair (a, b) of relation R is called the range of R.
Number of relations
- The total number of relations which can be defined from a set A to a set B is the number of possible subsets of A × B.
- A × B can have 2mn subsets. This means there are 2mn relations from A to B.
Representation of Relation
- Relation can be represented algebraically and graphically. The various methods of representation are as follows:
- Inverse of a relation
For any binary relation R, an inverse relation can be constructed by merely interchanging first and second components in every ordered pair.
It is denoted by R–1. Thus, R–1 = {(y, x) : (x, y) Î R}
- Types of Relations
Let A be a non-empty set. Then, a relation R on A is said to be
- Reflexive if (a, a) Î R for every aÎ A, i.e. if a R a for every a ∈ A.
- Symmetric if (a, b) Î R ⇒ (b, a) Î R for all a, b Î A, i.e. if a R b ⇒ b R a for all a, b Î A.
- Transitive if (a, b), (b, c) Î R ⇒ (a, c) Î R for all a, b, c Î A, i.e. if a R b and b R a ⇒ a R c.
- Equivalence Relation if it is reflexive, symmetric and transitive.
Download complete content for FREE 

