Coordinate Geometry
Coordinate Geometry Synopsis
Synopsis
- Coordinate axes
Two perpendicular number lines intersecting at point zero are called coordinate axes. The point of intersection is called origin and denoted by ‘O’. The horizontal number line is the x-axis (denoted by X’OX) and the vertical one is the y-axis (denoted by Y’OY).
- Cartesian plane
It is a plane formed by the coordinate axes perpendicular to each other in the plane. It is also called as xy plane.
The axes divide the Cartesian plane into four parts called the quadrants (one fourth part), numbered I, II, III and IV anticlockwise from OX.
Coordinates of a point
- The x-coordinate of a point is its perpendicular distance from y-axis, called abscissa.
- The y-coordinate of a point is its perpendicular distance from x-axis, called ordinate
- If the abscissa of a point is x and the ordinate of the point is y, then (x, y) is called the coordinates of the point.
- The point where the x-axis and the y-axis intersect is represented by the coordinate point (0, 0) and is called the origin.
Sign of the coordinates in the quadrants:
Sign of coordinates depicts the quadrant in which it lies.
- The point having both the coordinates positive i.e. of the form (+, +) will lie in the first quadrant.
- The point having x-coordinate negative and y-coordinate positive i.e. of the form (-, +) will lie in the second quadrant.
- The point having both the coordinates negative i.e. of the form (-, -) will lie in the third quadrant.
- The point having x-coordinate positive and y-coordinate negative i.e. of the form (+,-) will lie in the fourth quadrant.
- Coordinates of a point on the x-axis or y-axis:
The coordinates of a point lying on the x-axis are of the form (x, 0) and that of the point on the y-axis are of the form (0, y).
Distance formula
- The distance formula is used to find the distance between two any points say P(x1, y1) and Q(x2, y2) which is given by:
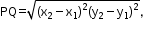
- The distance of a point P(x, y) from the origin O(0, 0) is

- The points A, B and C are collinear if AB + BC = AC.
Determining the type of triangle using distance formula
- Three points A, B and C are the vertices of an equilateral triangle if AB = BC = CA.
- The points A, B and C are the vertices of an isosceles triangle if AB = BC or BC = CA or CA = AB.
- Three points A, B and C are the vertices of a right triangle if the sum of the squares of any two sides is equal to the square of the third side.
Determining the type of quadrilateral using distance formula
For the given four points A, B, C and D, if:
- AB = CD, BC = DA; AC ¹ BD ⟹ ABCD is a parallelogram.
- AB = BC = CD = DA; AC ¹ BD ⟹ ABCD is a rhombus.
- AB = CD, BC = DA; AC = BD ⟹ ABCD is a rectangle.
- AB = BC = CD = DA; AC = BD ⟹ ABCD is a square.
- Section formula
- If P is a point lying on the line segment joining the points A and B such that AP: BP = m: n. Then, we say that the point P divides the line segment AB internally in the ratio m: n.
Coordinates of a point which divides the line segment joining the points (x1, y1) and (x2, y2) in the ratio m: n internally are given by:
This is known as the section formula.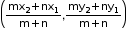
- If P is a point lying on AB produced such that AP: BP = m: n, then point P divides AB externally in the ratio m: n.
- If P divides the line segment joining the points A (x1,y1) and B(x2,y2) in the ratio m: n externally, then the coordinates of point P are given by
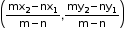 .
.
- Coordinates of Mid-point
Mid-point divides the line segment in the ratio 1:1. Coordinates of the mid-point of a line segment joining the points (x1, y1) and (x2, y2) are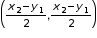
- Centroid of a triangle
- The point of intersection of the three medians of a triangle is called the centroid.
In the figure, G is the centroid of the triangle ABC where AD, BF and CE are the medians through A, B and C respectively.
Centroid divides the median in the ratio of 2:1.
- Coordinates of the centroid
If A(x1, y1), B(x2, y2) and C(x3, y3) are the vertices of a triangle ABC, then the coordinates of the centroid are given by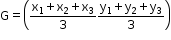
- Incentre of a triangle
- The point of intersection of all the internal bisectors of the angles of a triangle is called the incentre.
It is also the centre of a circle which touches all the sides of a triangle (such type of a circle is named as the incircle).
In the figure, I is the incentre of the triangle ABC.
- Coordinates of incentre
If A(x1, y1), B(x2, y2) and C(x3, y3) are the vertices of a triangle, then the coordinates of incentre are given by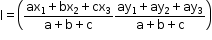
- Orthocentre of a triangle
The point of intersection of all the perpendiculars drawn from the vertices on the opposite sides (called altitudes) of a triangle is called the Orthocentre which can be obtained by solving the equations of any two of the altitudes.
In the figure, O is the orthocentre of the triangle ABC.
- Relation between Centroid, Incentre, Circumcemtre and Orthocenter
- If the triangle is equilateral, the centroid, the incentre, the orthocenter and the circumcentre coincides.
- Orthocentre, centroid and circumcentre are always collinear, whereas the centroid divides the line joining the orthocentre and the circumcentre in the ratio of 2:1.
- Area of a triangle
If A(x1, y1), B(x2, y2) and C(x3, y3) are the vertices of a triangle, then the area of triangle ABC is given by
Three given points are collinear, if the area of triangle formed by these points is zero.
- Area of a quadrilateral
Area of a quadrilateral can be calculated by dividing it into two triangles.
Area of quadrilateral ABCD = Area of ΔABC + Area of ΔACD
Note: To find the area of a polygon, divide it into triangular regions having no common area, then add the areas of these regions.
- Angle of Inclination and Slope of a Line
- Angle of Inclination
- The angle (say) θ made by the line ℓ with the positive direction of the x-axis and measured anticlockwise is called the inclination of the line. 0° ≤ θ ≤ 180°.
- A line which is parallel to the x-axis or coinciding with the x-axis has inclination 0°.
- A line which is parallel to the y-axis or coinciding with the y-axis has inclination 90°.
Slope of a Line
- The slope of a straight line is a measure indicating its inclination with respect to the positive direction of the x-axis.
- If q is the inclination of a line L, then tanq is called the slope or gradient of line L.
- Consider a line not parallel to the y-axis. If it makes an angle q with the x-axis (measured in the anticlockwise direction), then m = tanq is called the slope of the line.
- Slope of a line parallel to the y-axis is not defined.
- Slope of a line parallel to the x-axis is zero.
- If the slope is positive, then the angle of inclination q is an acute angle.
- If the slope is zero, then the line is the x-axis or is parallel to the x-axis.
- If the slope is negative, then the angle of inclination q is an obtuse angle.
- Slope or gradient of a line joining (x1, y1), (x2, y2) is
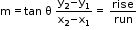
Parallel and Perpendicular lines
- Parallel lines
Two lines are parallel, i.e. they never meet, if and only if one of the following conditions holds:
- They are both vertical lines, i.e. they are parallel to the y-axis.
- If their slopes are equal, i.e. m1 = m2.
- Two lines (neither parallel to the y-axis) are perpendicular if and only if their slopes m1 and m2 satisfy the condition m1m2 = −1. If one of the lines is parallel to the y-axis, i.e. a vertical line with its slope undefined, then any line parallel to the x-axis, i.e. a horizontal line with slope 0 is perpendicular to it.
- Collinear Points
If X, Y and Z are three points in the XY plane, then they are collinear if and only if slope of XY is the same as the slope of YZ
- Horizontal and Vertical Lines
- Horizontal Line
If a horizontal line L is at a distance a units from the x-axis, then the ordinate of every point lying on the line is ‘a’. Thus, the equation of such a line L is y = a, where ‘a’ is any real number.
- Vertical Line
Equation of a vertical line at a distance b from the y-axis is x = b. Depending upon whether the line is to the left or right of the y-axis, the constant b is positive or negative.
- General form of Equation of Line
The general equation of a straight line is Ax + By + C = 0, where A, B and C are constants and A and B are not zero simultaneously.
Case 1: A ¹ 0, B = 0
In this case, the equation reduces to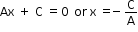
which is a straight line parallel to the y-axis.
Case 2: If A = 0, B 0, then the straight line is parallel to the x-axis.
By + C = 0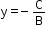
Case 3: A ¹ 0, B ¹ 0
In this case, the equation may be written as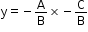
which is the slope intercept form of a straight line with slope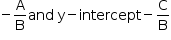
Case 4: If C = 0, then Ax + By + C = 0 becomes
Ax + By = 0.
This is a line passing through the origin and therefore the line has zero intercepts on the axes.
- Equation of a line parallel to the line Ax + By + C = 0 is Ax + By + K = 0, where K is any arbitrary constant.
- Equation of a line perpendicular to the line Ax + By + C = 0 is Bx − Ay + K = 0.
- Two or more lines are concurrent if they meet at a single point.
- Various forms of equation of line
General equation of line Ax + By + C = 0 can be reduced to the other forms of line as: - Slope intercept form
If B ≠ 0, then Ax + By + C = 0 can be written as
By = −Ax − C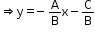
The standard equation in slope intercept form is y = mx + c where ‘m’ is the slope and ‘c’ is y-intercept.
If line L with slope m makes x-intercept as d. The equation of line is y = m(x − d).
- Point - slope form
Let ‘m’ be the slope and (x0,y0) be the point lying on the same line, then
Equation of line will be y - y0 =m( x- x0)
- Two-points form
The equation of the line passing through the points (x1, y1) and (x2, y2) is given by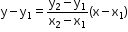
- Intercept form
If C ≠ 0, then Ax + By + C = 0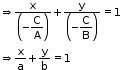
Thus, equation of the line making intercepts a and b on the X and Y axes, respectively is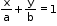
- Normal form
Ax + By + C = 0 or Ax + By = −C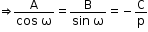
 is the equation of line in normal form
is the equation of line in normal form
Here, p is the normal distance of a line from the origin and w is the angle made by a line with positive x-axis.
- Distance Form
Equation of line in distance form is given by: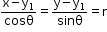
Here, ‘r’ is the distance of the point (x, y) on the line from the point (x1,y1), Ѳ is the angle with the positive direction of the x-axis.
- The equation of the lines passing through (x1,y1), and making an angle Ѳ with the line y = mx +c is given by
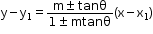
Distance of a Point from a Line
- The coordinates of any point on the line at a distance r from the point (x1,y1) are
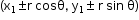
- The distance of a point from a line is the length of the perpendicular drawn from the point on the line.
- The perpendicular distance (d) of a line Ax + By + C = 0 from a point P(x1, y1) not on it is given by
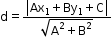
Distance between two Lines
- Distance between two parallel lines is equal to the length of the perpendicular from a point on line 1 to the point on line 2.
- Therefore, the distance between the parallel lines y = mx + c and y = mx + d is given by
Distance =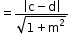
- Coincident and Collinear Lines
- If two lines having the same slope pass through a common point, then the two lines will coincide.
- Let L1= a1x + b1y + c1 =0 ,L2 = a2x+ b2y+c2 = 0 and L3= a3x + b3y +c3 =0, be three lines.
These lines are concurrent if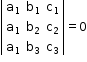
- Angle between two lines
Let L1= a1x + b1y + c1 =0 and L2 = a2x+ b2y+c2 = 0 be the two intersecting lines.
The angle (say θ) between the two lines is given by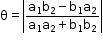
Download complete content for FREE 

