Plane Geometry–Triangles
Plane Geometry - Triangles Synopsis
Synopsis
- Introduction to Triangles
- A triangle is a simple closed figure made up of three line segments.
- It has six parts or elements, namely: a) Three sides and b) Three angles.
- The point of intersection of two adjacent sides of a triangle is called a vertex. A triangle has 3 vertices.
- Median of a Triangle
- A median of a triangle is the line segment joining a vertex of the triangle to the mid-point of its opposite side. A triangle has three medians.
Here AD is the median corresponding to the side BC. - A triangle has three medians and all the three medians are always concurrent.
- Centroid of a Triangle
- The point of intersection of the medians is called the centroid of the triangle.
Here, G is the centroid of the triangle ABC. - Centroid of a triangle divides each median in the ratio 2 : 1.
From the figure, AG : GD = 2 : 1; BG : GE = 2 : 1; and CG : GF = 2 : 1
- Altitude of a Triangle
- An altitude of triangle is the perpendicular drawn from a vertex of a triangle to its opposite sides.
- A triangle has three altitudes.
Here Ad is the altitude corresponding to the side BC. - A triangle has three altitudes and all the three altitudes are always concurrent.
- The point of intersection of the altitudes of a triangle is called the orthocenter.
Here, O is the orthocenter of the triangle ABC.
Properties of Triangles
- The sum of the three interior angles of a triangle is always 180o
- The measure of an exterior angle is equal to the sum of the measures of the interior opposite angles.
- The measure of an exterior angle is greater than the measure of each of the interior opposite angles.
- The sum of the measure of exterior angle at a vertex and its adjacent interior angle is 180o.
Triangle Inequalities
- Sum of any two sides of a triangle is always greater than the third side.
- The difference of any two sides is always less than the third side.
- If two sides of a triangle are not equal, then the angle opposite to the greater side is greater and vice versa.
- Let a, b, c be the three sides of a triangle ABC where AB = c is the longest side. Then,
- If c2 < a2 + b2, then the triangle is acute angled.
- If c2 = a2 + b2, then the triangle is right angled.
- If c2 > a2 + b2, then the triangle is obtuse angled.
Relation between sides angles of a triangle
- If all the sides of a triangle are of different lengths, its angles are also of different measures in such a way that the greater side has greater angle opposite to it.
- The greater angle has greater side opposite to it.
- If any two sides of a triangle are equal, the angles opposite to them are also equal.
- If any two angles of a triangle are equal, the sides opposite to them are also equal.
- If all the sides of a triangle are equal, all its angles are equal.
- If all the angles of triangle are equal, all its sides will also be equal.
- Sine and Cosine Rules
- Sine Rule
In a ∆ABC, if a, b and c be the three sides opposite to the angles A, B and C respectively, then
- Cosine Rule
In a ∆ABC, if a, b and c be the three sides opposite to the angles A, B and C respectively, then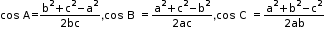
Theorems on Triangles
- Basic Proportionality Theorem (BPT)
If a line is drawn parallel to one side of a triangle to intersect other two sides in distinct points, the other two sides are divided in the same ratio. - Converse of BPT
If a line divides any two sides of a triangle in the same ratio then the line is parallel to the third side. - Mid-point Theorem
A line drawn through the mid-point of one side of a triangle which is parallel to another side bisects the third side. - Converse of Mid-point Theorem
The line segment joining the mid-points of two sides of a triangle is parallel to the third side and equal to one-half of it. - Apollonius Theorem
In a triangle, the sum of the squares of any two sides of a triangle is equal to twice the sum of the square of the median to the third side and square of half the third side.
- Interior Angle Bisector Theorem
In a triangle, the angle bisector of an angle divides the opposite side to the angle in the ratio of the remaining two sides.
- External Angle Bisector Theorem
In a triangle, the angle bisector of any exterior angle of a triangle divides the side opposite to the external angle in the ratio of the remaining two sides. - Pythagoras Theorem
In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Thus, in triangle ABC right angled at B, AB2 + BC2 = AC2
- Converse of Pythagoras Theorem
If in a triangle, square of one side is equal to the sum of the squares of the other two sides, then the angle opposite the first side is a right angle
Congruent figures
- Two figures are said to be congruent, if they are of the same shape and of the same size.
- Two circles of the same radii are congruent.
- Two squares of the same sides are congruent.
- Congruent triangles
- Two triangles are said to be congruent to each other, if all the sides and angles of one triangle are equal to the corresponding sides and angles of another triangle.
- The symbol is read as "is congruent to"
- Congruent triangles always coincide by superposition.
- In congruent triangles, the sides and angles that coincide by superposition are called corresponding sides and corresponding angles.
- The corresponding sides lie opposite to the equal angles and corresponding angles lie opposite to the equal sides.
- In congruent triangles, corresponding parts are equal. We write in short ‘C P C T C ’ for corresponding parts of congruent triangles.
- Conditions of Congruency
- SAS congruence condition:
Two triangles are congruent if two sides and the included angle of one triangle are equal to the two sides and the included angle of the other triangle.
by SAS congruency criteria.
- ASA congruence condition:
Two triangles are congruent if two angles and the included side of one triangle are equal to two angles and the included side of other triangle.
by ASA congruency criteria.
- AAS congruence condition:
Two triangles are congruent if any two pairs of angles and one pair of corresponding sides are equal.
by AAS congruency criteria
- SSS congruent condition:
If three sides of one triangle are equal to the three sides of another triangle, then the two triangles are congruent.
by SSS congruency criteria
- RHS congruence condition:
If in two right triangles the hypotenuse and one side of one triangle are equal to the hypotenuse and one side of the other triangle, then the two triangles are congruent.
Here, ΔABC ≅ ΔQRP by RHS congruency criteria.
- Similar figures:
- Two figures are similar, if they are of the same shape but not necessarily of the same size.
- All congruent figures are similar but the similar figures need not to be congruent.
- Similarity of Triangles
- Two triangles are similar (~) if their corresponding angles are equal and their corresponding sides are in same ratio.
- If the angles in two triangles are:
- Different, the triangles are neither similar nor congruent.
- Same, the triangles are similar.
- Same and the corresponding sides are of the same size, the triangles are congruent.
Tests of Similarity
- AAA (Angle-Angle-Angle) similarity criterion:
If in two triangles, corresponding angles are equal, then their corresponding sides are in the same ratio (or proportion) and hence the two triangles are similar.
- AA (Angle-Angle) similarity criterion:
If two angles of a triangle are respectively equal to two angles of another triangle, then by the angle sum property of a triangle their third angles will also be equal.
Thus, AAA similarity criterion changes to AA similarity criterion which can be stated as follows:
If two angles of one triangle are respectively equal to two angles of other triangle, then the two triangles are similar. - Converse of AAA similarity criterion:
If two triangles are similar, then their corresponding angles are equal.
- SSS (Side-Side-Side) similarity criterion:
If in two triangles, sides of one triangle are proportional to (i.e., in the same ratio of) the sides of the other triangle, then their corresponding angles are equal and hence the two triangles are similar.
- Converse of SSS similarity criterion:
If two triangles are similar, then their corresponding sides are in constant proportion.
- SAS (Side-Angle-Side) similarity criterion:
If one angle of a triangle is equal to one angle of the other triangle and the sides including these angles are proportional, then the two triangles are similar.
- Converse of SAS similarity criterion:
If two triangles are similar, then one of the angles of one triangle is equal to the corresponding angle of the other triangle and the sides including these angles are in constant proportion.
- RHS (Right angle-Hypotenuse-Side) criterion:
If in two right triangles, hypotenuse and one side of one triangle are proportional to the hypotenuse and one side of another triangle, then the two triangles are similar. This criteria is referred as the RHS similarity criterion.
Properties of Similar Triangles
- The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
Thus, if Δ ABC ~ Δ PQR, then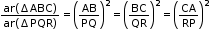
- In a right angled triangle, the triangles on each side of the altitude drawn from the vertex to the right angle to the hypotenuse are similar to the original triangle and to each other too.
i.e., ∆BCA ~ ∆BDC ~ ∆CDA.
- Area of Triangles
- General Formula: Area of a triangle

- Area of a scalene triangle
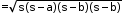
where a, b, c are sides of the triangle and semi-perimeter
- Area of a right angled triangle

For a right angled triangle,
- Inradius
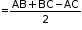 where triangle ABC is right angled at B
where triangle ABC is right angled at B - Inradius
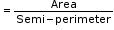
- Circum radius
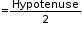
- Area of an isosceles triangle
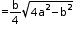 where a is the length of one of the equal sides, b is the length of third side.
where a is the length of one of the equal sides, b is the length of third side. - For an equilateral triangle,
- Area
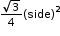
- Inradius
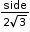
- Circumradius
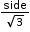
Therefore, Circumradius = 2 × Inradius
Download complete content for FREE 

