Permutations and Combinations
Permutations and Combinations Synopsis
Synopsis
Fundamental principles of counting
- Multiplication Principle
If an event can occur in m different ways, following which another event can occur in n different ways, then the total number of occurrences of the events in the given order is m x n. This principle can be extended to any number of finite events. The keyword here is ‘and’.
- Addition Principle
If there are two jobs such that they can be performed independently in m and n ways respectively, then either of the two jobs can be performed in (m + n) ways. This principle can be extended to any number of finite events. The keyword here is ‘OR’.
- Factorial notation
The notation ‘n!’ represents the product of first ‘n’ natural numbers i.e. n! = 1 x 2 x 3 x 4 x … x n.
Permutation
- A permutation is an arrangement in a definite order of a number of objects taken some or all at a time.
- In permutations, the order is important.
- Keyword for permutations is ‘arrangement’.
Number of Permutations
- The number of permutations of ‘n’ different objects taken ‘r’ at a time, where 0 < r ≤ n and the objects do not repeat is n(n – 1)(n – 2). . . (n – r + 1) denoted by nPr.
- The number of permutations of ‘n’ different objects taken ‘r’ at a time, where repetition is allowed is nr.
- The value of nPr without repetition is given by

Permutations of Alike Things
- The number of permutations of ‘n’ objects, taken all at a time, where ‘p’ objects are alike of one kind and ‘q’ objects are alike of second kind such that p + q = n, is given by
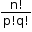 .
. - The number of permutations of ‘n’ objects, where p1 are alike of one kind, p2 are alike of second kind, … pk are alike of kth kind such that , is
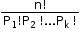 .
. - The number of permutations of ‘n’ objects, where ‘p’ objects are of one kind, ‘q’ are alike of second kind and remaining all are distinct is given by
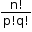 .
. - Assume that there are ‘k’ things to be arranged with repetitions. Let p1, p2, p3, … pk are integers such that the first object occurs exactly p1 times, the second occurs exactly p2 times…, then the total number of permutations of these ‘k’ objects with the above condition is
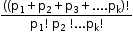 .
.
Circular permutation
- When clockwise and anti-clockwise arrangements are different:
Number of permutations: (n - 1)! - When clockwise and anti-clockwise arrangements are the same:
Number of permutations: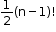
- Number of circular permutations of n different things taken r at a time when clockwise and anticlockwise arrangements are taken as different is
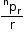 .
. - Number of circular permutations of n different things, taken r at a time, when clockwise and anticlockwise arrangements are not different
 .
.
Permutation under restrictions
Selecting and arranging r distinct objects from n
- When ‘k’ particular things are always to be included.
Number of permutations:
- When a particular thing is always to be included (k = 1).
Number of permutations: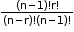
- When ‘k’ particular things are never included.
Number of permutations: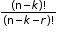
- When a particular thing is never included.
Number of permutations: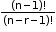
- When ‘l’ particular things always come together.
Number of permutations: (n -l + 1)! x l! - When ‘l’ particular things never come together.
Number of permutations: n! -(n - l + 1)! x l!
- Combination
Combination is a way of selecting objects from a group, irrespective of their arrangements.
Keyword for combination is ‘selection’.
- Difference between Permutations and Combinations:
Number of Combinations
- The number of combinations or selection of ‘r’ different objects out of ‘n’ given different objects is nCr, which is given by
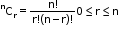
- Number of combinations of ‘n’ different things, without taking any of them, is considered to be 1.
- Counting combinations is merely counting the number of ways in which some or all objects are selected at a time.
- Selecting ‘r’ objects out of ‘n’ objects is the same as rejecting (n – r) objects, so nCn – r ꞊ nCr.
- Ways of selecting one or more things at a time is
Number of combinations: nC1+ nC2+ Cn = 2n-1 - When ‘k1’ alike objects of one kind, ‘k2’ alike objects of the second kind … ‘kn’ alike objects of the nth kind.
Number of combinations: (k1+1)(k2+1)…(kn+1)-1 - When ‘k1’ alike objects of one kind, ‘k2’ alike objects of the second kind … ‘kn’ alike
objects of the nth kind and rest ‘p’ elements are different.
Number of combinations:(k1+1)(k2+1)…(kn+1)]2p-1
Combinations under restriction
- When ‘k’ particular things are always to be included
Number of combinations: (n-k)C(r-k) - When a particular thing is always to be included (k = 1)
Number of combinations: (n-1)C(r-1) - When ‘k’ particular things are never included
Number of combinations:(n-k)Cr - When ‘k’ particular things never come together
Number of combinations:nCr -(n-k)C(r-k)
Key Formulae
- n! = 1 x 2 x 3 x …x n or n! = n x (n -1)!
- n! is defined for positive integers only.
- n! = n(n – 1)(n – 2)! (provided n ³ 2)
- n! = n(n – 1)(n – 2)(n – 3)! (provided n ³ 3)
- 0! = 1! = 1
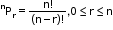
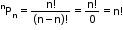
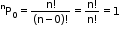
- If Pm represents mPm, then 1+1.P1+2.P2+3.P3+…+n.Pn=(n+1)!
-
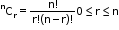
- nCx= nCy ⟺ x + y = n or x = y
- Pascal’s Rule: If ‘n’ and ‘k’ are non-negative integers such that k ≤ n , then nCk+nCk-1 = n+1Ck
- If ‘n’ and ‘k’ are non-negative integers such that 1 ≤ k ≤ n , then
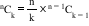
- If ‘n’ and ‘k’ are non-negative integers such that 1 ≤ k ≤ n , then k⨯(nCk)=(n-k+1)⨯nCk-1
- The greatest among nC0,nC1,nC2,…ncn is
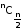 when ‘n’ is an even natural number.
when ‘n’ is an even natural number. - The greatest among nC0,nC1,nC2,…ncn is
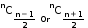 , when ‘n’ is an odd natural number.
, when ‘n’ is an odd natural number. - nPr = nCr r!, 0
- nC0 = nCn =1
- nCn-1 = nC1 =n
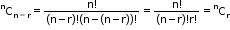
Download complete content for FREE 

