Logarithms
Logarithms Synopsis
Synopsis
Related Terms
- Let a, b, c are three numbers and they are related so that ab = c ; then exponent, 'b' is called the logarithm of number, 'c' to the base 'a', and loga c= b
- Definition of logarithm: Thus, logarithm of any number to a given base is equal to the index to which the base should be raised to get the given number.
Important points
- The exponential form: ab = c
- Logarithmic form: loga c = b
- When x0 = 1 ⟹ logx 1 = 0
- Logarithm of 1 to any base is zero.
- Since,a1 =a,loga a =1
- Logarithms to the base 10 are known as common logarithms.
- If no base is given, the base is always taken as 10.
- If a and x are positive real numbers, where a ≠ 1, then alogax =x
- For a > 0, a ≠ 1, loga x =logb y ⟹ x= y (x,y>0).
- If a > 1 and x > y, then loga x > loga y
- If 0 < a < 1 and x > y, then loga x > loga y
Laws of Logarithms
For m,n, a > 0 and a ≠ 1
- Product Law: The logarithm of a product is equal to the sum of the logarithms of its factors.
i.e. loga (m × n) = loga m + loga n - Quotient Law: The logarithm of fraction is equal to the difference between the logarithm of the numerator and the logarithm of the denominator.
loga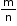 = loga m – loga n
= loga m – loga n - Power Law: The logarithm of a power of a number is equal to the logarithm of the number multiplied by the power.
loga mn = n loga m
- Logarithm of a number x to the base a is equal to 1 divided by logarithm of a to the base x.
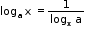
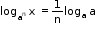
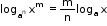
- logax = logb x loga b
- xloga y = ylogax
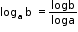
- If logab =x for all a > 0, a ≠ 1, b > 0 and x ∈ R, then log1/a b = - x, loga 1/b = - x and log1/a 1/b= x
Download complete content for FREE 

