Probability
Probability Synopsis
Synopsis
Introduction to Probability
- The theory of probability is a branch of mathematics which deals with uncertain or unpredictable events. Probability is a concept which gives a numerical measurement for the likelihood of occurrence of an event.
- An act which gives some result is an experiment.
- The possible result of an experiment is called its outcome.
The sample space S of an experiment is the set of all its outcomes. Thus, each outcome is also called a sample point of the experiment.
An experiment is called random experiment if it satisfies the following two conditions:
- It has more than one possible outcome.
- It is not possible to predict the outcome in advance.
- Deterministic experiment
An experiment which results in a unique outcome.
- Event
Sample space is a set consisting of all the outcomes; its cardinality is given by n(S). Any subset ‘E’ of a sample space for an experiment is called an event.
- Probability of an event
Probability of an event E is the ratio of the number of elements in the event to the number of elements in the sample space.
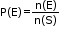
- 0 ≤ P(E) ≤ 1
Types of Events
- Sure Event
The empty set f and the sample space S describe events. In fact, f is called an impossible event and S, i.e. the whole sample space, is called a sure event. - Simple Event
If an event E has only one sample point of a sample space, it is called a simple (or elementary) event. - Compound Event
A subset of the sample space which has more than an element is called a compound event. - Equally likely events
Events are said to be equally likely if we have no reason to believe that one is more likely to occur than the other. Both outcomes (head and tail) of tossing a coin are equally likely. - Certain event (sure event)
If a random experiment occurs always, then the corresponding event is called a certain event.
Impossible event
If a random experiment never occurs, then the corresponding event is called an impossible event. - Mutually exclusive event
In a random experiment, if the occurrence of any one event prevents the occurrence of all the other events, then the corresponding events are said to be mutually exclusive.In other words, events A and B are said to be mutually exclusive if and only if they have no elements in common.
- Exhaustive event
In a random experiment, if the union of two or more events is the sample space, then the associated events are said to be exhaustive events.
In other words, when every possible outcome of an experiment is considered, the events are called exhaustive events.
- Independent events
Two or more events are said to be independent if the occurrence or non-occurrence of any of them does not affect the probability of occurrence or non-occurrence of the other events.
Complement of an event
The complement of an event A is the set of all outcomes which are not in (or not favourable to) A. It is denoted by A’.
Algebra of Events
- Intersection of Events
If A and B are events, then the event 'A and B' is defined as the set of all the outcomes which are favourable to both A and B, denoted by A ∩ B. This is represented diagrammatically as follows.
(A ∩ B ∩ C) is the event that occurs when all the three events A, B and C occur.
- Union of Events
When the sets A and B are two events associated with a sample space, then ‘A È B’ is the event ‘either A or B or both’. Therefore, Event ‘A or B’ = A È B = {w : wÎ A or w Î B}
(A ∪ B ∪ C) is the event that occurs when at least one of the events A, B or C occurs.
- Difference of Events
If A and B are events, then the event 'A – B' is defined to be the set of all outcomes which are favourable to A but not to B. A – B = A Ç B’ = {x: x ∈ A and x ∈ B}
This is represented diagrammatically as:
- As mutually exclusive events cannot occur together, if events A and B are mutually exclusive, then A ∩ B = ϕ since A and B have nothing in common.
- Mutually exclusive and exhaustive events
Events E1, E2, ..., En are mutually exclusive and exhaustive if E1 È E2 È….È En = S and Ei ∩ Ej = φ, for every distinct pair of events
- If S is the sample space of an experiment with n equally likely outcomes S = {w1, w2, w3, …, wn} then
- P(w1) = P(w2) = … = P(wn) = n
-
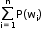 = 1, so P(wn) = 1/n
= 1, so P(wn) = 1/n
Addition Theorem of probability
- Addition Theorem for 2 events
- If ‘A’ and ‘B’ be any two events, then the probability of occurrence of at least one of the events ‘A’ and ‘B’ is given by: P(AÈB) = P(A) + P(B) – P (A Ç B).
- If A and B are mutually exclusive events then P(A È B) = P(A) + P(B)
- Addition Theorem for 3 events
- If A, B and C are three events associated with a random experiment, then
P(AÈBÈC) = P(A) + P(B) + P(C) - P(AÇB) - P(BÇC) - P(AÇC) + P(AÇBÇC) - If ‘E’ is any event and E’ is the complement of event ‘E’, then P(E’) = 1 – P(E)
- Addition theorem in terms of difference of events
P(A È B) = P(A – B) + P(B – A) + P(A Ç B) - Probability of difference of events
Let A and B be any two events then, P(A – B) = P(A) – P(A ÇB).
- Operations on Probability of Events
- If A and B are two events, then the probability of occurrence of A only is
P(A Ç B) = P(A) – P) (A Ç B) - If A and B are two events, then the probability of occurrence of B only is
P(A Ç B) = P(B) – P) (A Ç B - If A and B are two events, then the probability of occurrence of exactly one of A and B is
P(A Ç B) + P( (A Ç B)=P (A) + P (B) – 2P (A Ç B) = P (AÈB) – P (A Ç B) - If A and B are two events associated to a random experiment such that , then A ⊂ B, then A Ç B≠ ϕ
- If A and B are two events, then P (A ÇB) = P(A) ≤ P (A È B) ≤ P (A) = P(B)
- Probability of Independent Events
- If two events, A and B, are independent P (A and B) = P (A) × P (B).
i.e. P (A ∩ B) = P (A) × P (B) - If A, B, C are independent events, then P (A and B and C) = P (A) × P (B) × P (C)
i.e. P (A ∩ B ∩ C) = P (A) × P (B) × P (C). - In general, if A1, A2, ..... An are n independent events, then
P (A1 ∩ A2 ∩ A3 ..... ∩ An) = P (A1) × P (A2) ..... × P (An)
Download complete content for FREE 

