Inequalities
Inequalities Synopsis
Synopsis
Introduction to inequations
- An inequation is a mathematical statement which states that one quantity is not equal to the other, which means less than or greater than the other quantity.
- In an inequation, the signs, are called signs of inequality.
Rules for solving in equations algebraically:
- On transferring a positive term (the term in addition) from one side of an inequation to its other side, the sign of the term becomes negative.
Example: 5x + 3 ≤ 13 ⟹ 5x ≤ 13 - 3 - On transferring a negative term from one side of an inequation to its other side, the sign of the term becomes positive.
Example: 5x - 3 ≤ 13 ⟹ 5x ≤ 13+3 - If each term of an inequation be multiplied or divided by the same positive number, the sign of inequality remains the same.
Case I: If p is positive and x < y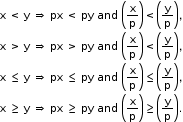
- If each term of an inequation be multiplied or divided by the same negative number, the sign of inequality reverses.
Case II: If p is negative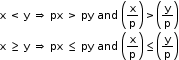
Example: x ≤ -2 ⟹ (-3) × x ≥(-3) × (-2) ⟹ 3x ≥ 6 - If sign of each term on both the sides of an inequation is changed, the sign of inequality gets reversed.
Example: -3 x ≥ 20 ⇒ 3x ≤ - 20 - If both the sides of an inequation are either positive or negative, then on taking their reciprocals, the sign of inequality reverses.
Example: If x and y both are either positive or negative, then - The sign of the inequality does not change when a positive number is added or subtracted to both the sides.
i. If x < y, then x + a < y + a.
ii. If x < y, then x – a < y – a. - The sign of the inequality does not change when a positive power is raised on both the sides.
i. If m > 0 and a > b > 0, then am > bm
ii. If m > 0 and a < b, a > 0, b > 0, then am < bm - The sign of the inequality does not change when reciprocal of a positive power is raised on both the sides.
i. If m > 0 and a > b > 0, then a1/m > b1/m
ii. If m > 0 and a < b, a > 0, b > 0, then a1/m < b1/m - The sign of the inequality changes when a negative power is raised on both the sides.
i. If m > 0 and a > b > 0, then a–m < b–m
ii. If m > 0 and a < b, a > 0, b > 0, then a–m > b–m - If a > 1 and m > 0, then
i. am > 1
ii. 0 < a–m < 1 - If 0 < a < 1 and m > 0, then
i. 0 < am < 1
ii. a–m > 1 - If a > 1 and m > n > 0, then am > an
- If 0 < a < 1 and m > n > 0, then am < an
- If 0 < a < 1 < b and r is a positive rational number, then
i. 0 < ar < 1 < a–r
ii. 0 < b–r < 1 < br - If a > 1 and x > y > 0, then loga x > loga y
- If 0 < a < 1 and x > y > 0, then loga < loga y
Replacement Set and Solution Set
1.Replacement set is the set from which the values of the variable involved in the inequation are chosen.
2.Solution set is the subset of the replacement set, whose elements satisfy the given inequation.
Example: Let the given inequation be x ≤ 4, if:
- iThe replacement set = N, the set of natural numbers;
The solution set = {1, 2, 3, 4} - The replacement set = W, the set of whole numbers;
The solution set = {0, 1, 2, 3, 4} - The replacement set = Z or I, the set of Integers;
The solution set = {….-2, -1, 0, 1, 2, 3, 4} - The replacement set = R, the set of real numbers;
The solution set = { x:x ϵ R and x ≤ 4}
3. The solution set depends on the replacement set.
Representation of the solution on the number line:
- The solution set of an inequation can be represented on a real number line.
- A hollow circle marks the end of a range with a strict inequality (< or >).
- A darkened circle marks the end of a range involving an equality as well (≤ or ≥ ).
- Some examples:
Download complete content for FREE 

